Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chào em Hoàng Thị Thu Huyền, em học là học lớp mấy, em học trường nào ? em học là học ra sao (lá là la) em học giỏi hay học dốt, em học giỏi quá cơ....
Chào em HTTH, em là quản lí của trang online math, trong diễn đàn, toàn trai (lá là la), em có thích ngắm trai ko, em mê trai quá cơ...
Sinh thay con HTTH, em ở cầy Giấy (í i i ì i í) con HTTH em dạy học .....
(còn nữa, chờ phần 2)
báo cáo làm dog

a/b=c/d =>a/c=b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)\(\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left(\frac{a+b}{b+d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow dpcm\)

1.Kết quả phép tính36.34.32 là:
A.272 B.312 C.348 D.30
2.Từ tỉ lệ thức \(\frac{a}{b}\)=\(\frac{c}{d}\)(a,b,c,d #0) ta có thể suy ra:
A.\(\frac{d}{b}\)=\(\frac{c}{a}\) B.\(\frac{a}{b}\)=\(\frac{c}{d}\)
C.\(\frac{a}{c}\)=\(\frac{d}{b}\) D.\(\frac{a}{d}\)=\(\frac{b}{c}\)
3.Nếu\(\sqrt{x}\)=4 thì x bằng:
A.\(\pm\)2 B.\(\pm\)6 C.\(\pm\)2 D.\(\pm\)16
Hok tốt!

P = |x – 2015| + |x – 2016| + |x – 2017|
P = (|x – 2015| + |2017 – x|) + |x – 2016|
Vì |x – 2015| + |2017 – x| \(\ge\) |x – 2015 + 2017 – x| = 2 với mọi x
=> (|x – 2015| + |2017 – x|) + |x – 2016| \(\ge\) 2 + |x – 2016| \(\ge\) 2 với mọi x
=> P \(\ge\) 2 với mọi x
Dấu “=” xảy ra ó x = 2016
Vậy minP = 2 tại x = 2016
Lâu chưa làm nên không chắc lắm

Ta có:
\(a< b,c< d,m< n\)
\(\Rightarrow a+c+m< b+d+n\Rightarrow2a+2c+2m< a+b+c+d+m+n\)
\(\Rightarrow a+c+m< \frac{1}{2}\left(a+b+c+d+m+n\right)\)
\(\Rightarrow\frac{a+c+m}{a+b+c+d+m+n}< \frac{1}{2}\) ( đpcm )

1)\(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}\)
\(A< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}\)(1)
\(A>\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{100.101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{101}\)
\(A>\dfrac{96}{505}>\dfrac{1}{6}\)
\(A>\dfrac{1}{6}\)(2)
Từ (1) và (2)
\(\dfrac{1}{6}< A< \dfrac{1}{4}\)
2)
\(A=\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{92.95}+\dfrac{1}{95.98}\)
\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{92}-\dfrac{1}{95}+\dfrac{1}{95}-\dfrac{1}{98}\right)\)\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{98}\right)\)
\(A=\dfrac{1}{3}.\dfrac{24}{49}=\dfrac{8}{49}\)

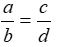 (a, b, c, d # 0) ta có thể suy ra:
(a, b, c, d # 0) ta có thể suy ra: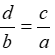 B.
B. 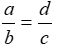
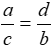 D.
D.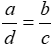
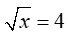 thì x bằng:
thì x bằng: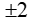 B.
B. 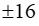 C. 2 D.16
C. 2 D.16



la sao ha ban ?
copy link đó và làm bài