Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)


Bài 2:
Quãng đường AB dài: \(S_{AB}=v\times t=40\times5=200\left(km\right)\)
thời gian ô tô chạy từ A đến B với vận tốc 50km/h là:
\(t=\frac{S}{v}=\frac{200}{50}=4\left(h\right)\)
Bài 3:
C D M B A
a,Xét ΔMAD và ΔMCB có
\(\begin{cases}AM=CM\left(gt\right)\\MD=MB\left(gt\right)\\\widehat{AMD}=\widehat{CMB}\end{cases}\)
→ΔMAD=ΔMCB(c.g.c)
b,theo câu a:ΔMAD=ΔMCB
\(\Rightarrow\begin{cases}AD=BC\\\widehat{MAD}=\widehat{MCB}\end{cases}\)
c,tứ giác ABCD có 2 đường chéo AC, BD cắt nhau tại trung điểm M mỗi đường
→ABCD là hình bình hành
→AB//CD
Bài 1:
Gọi số tiền lãi ba đơn vị nhận được lần lượt là x,y,z
theo đề bài ta có x:y:z=3:4:5 và x+y+z=225
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{225}{9}=25\)
do đó \(\begin{cases}x=3\times25=75\\y=4\times25=100\\z=5\times25=125\end{cases}\)
vậy...
Bài 5:
A B K C
vì ΔABC vuông cân tại A nên \(\widehat{B}=\widehat{C}=45^o\)
a, xét ΔAKB và ΔAKC có
\(\begin{cases}AB=AC\left(gt\right)\\KB=KC\left(gt\right)\\\widehat{B}=\widehat{C}=45^o\left(cmt\right)\end{cases}\)
→ΔAKB=ΔAKC(c.g.c)
b,ΔABC vuông tại A có AK là đường trung tuyến
→AK là đường cao
→AK vuông góc BC

Biết rằng parabol (P): y=ax2+bx-1 qua điểm A(3;-7) và có hoành độ đỉnh bằng 1. Tính giá trị của biểu thức 2a+b . Các bạn ơi đề bài bị sai dề bài này mới chính xác

mik 2k7 nhung co
bai j khong biet
ban se gui cho mik nhe!
mik lam cho

Câu 40: -6<2x<=8
=>-3<x<=4
=>A=(-3;4]
=>\(C_{R}A\) =R\A=(-∞;3]\(\cup\) (4;+∞)
|x+1|<=2
=>-2<=x+1<=2
=>-3<=x<=1
=>B=[-3;1]
=>\(C_{R}B\) =R\B=(-∞;-3)\(\cup\) (1;+∞)
\(\left(C_{R}A\right)\) \\(\left(C_{R}B\right)\) =[-3;1]
=>Không có câu nào đúng
Câu 39:
Để A giao B=rỗng thì -m+2>2m+1 hoặc -m+5<=2m-3
=>-3m>-1 hoặc -3m<=-8
=>m<1/3 hoặc m>=8/3
=>Chọn B
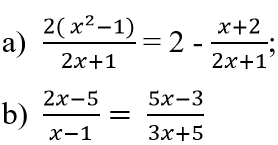

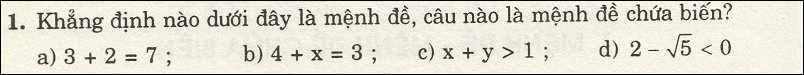


 Các bn giúp mk nhé
Các bn giúp mk nhé