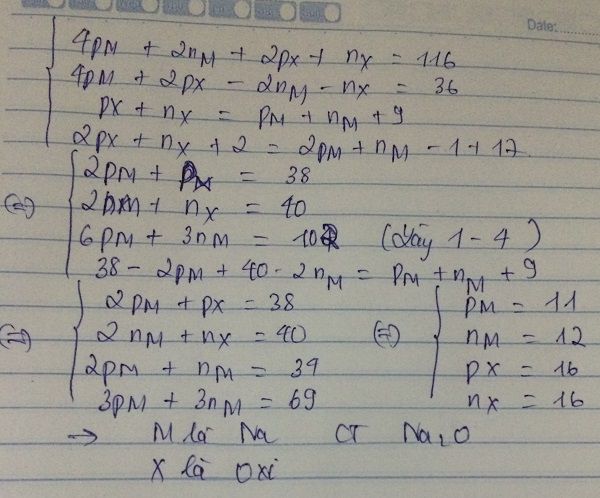Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng số hạt: 110 => 2ZM + NM + 2ZX + NX = 110 (1)
Hạt mang điện nhiều hơn hạt không mang điện là 34 => (2ZM + 2ZX) - (NM + NX) = 34 hay 2ZM - NM + 2ZX - NX = 34 (2)
Số khối của M+ lớn hơn số khối của X- là 14
=> ZM + NM - ZX - NX = 14 (3)
Số hạt của ion M+: 2ZM + NM - 1
Số hạt của ion X-: 2ZX + NX + 1
Theo đề bài ta lại có:
(2ZM + NM - 1) - (2ZX + NX + 1) = 4
hay 2ZM + NM - 2ZX - NX = 4 + 1 + 1 = 6 (4)
Từ (1), (2), (3), (4) ta suy ra:
ZM = 14, NM = 30, ZX = 22, NX = 8

Gọi số hạt của M là p1,n1,e1 ( p1 = e1 )
Gọi số hạt của X là p2,n2,e2 ( p2 = e2 )
\(\Sigma hatMX=110\)
\(\Leftrightarrow2p_1+2p_2+n_1+n_2=110\left(1\right)\)
Hạt mang điện nhiều hơn hạt không mang điện là 34:
\(\Leftrightarrow2p_1+2p_2-n_1-n_2=34\left(2\right)\)
Số khối \(M^+\) lớn hơn số khối \(X^-\) là 14
\(\Leftrightarrow p_1+n_1-p_2-n_2=14\left(3\right)\)
Số hạt ion \(M^+\) lớn hơn \(X^-\) là 4
\(\Leftrightarrow2p_1+n_1-1-\left(2p_2+n_2+1\right)=4\)
\(\Leftrightarrow2p_1-2p_2+n_1-n_2=6\left(4\right)\)
\(\left(1\right)+\left(2\right)\Rightarrow4p_1+4p_2=144\)
\(\left(4\right)-\left(3\right)\Rightarrow p_1-p_2=-8\)
\(\Rightarrow\left\{{}\begin{matrix}p_1=14\\p_2=22\end{matrix}\right.\)
=> SiTi :v
có sai chỗ nào không nhỉ???

Ta có:
\(\left\{{}\begin{matrix}2\left(Z_{X^{2-}}+Z_{M^{2+}}\right)+\left(N_{X^{2-}}+N_{M^{2+}}\right)=84\\2\left(Z_{X^{2-}}+Z_{M^{2+}}\right)-\left(N_{X^{2-}}+N_{M^{2+}}\right)=28\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}Z_{X^{2-}}+Z_{M^{2+}}=28\\N_{X^{2-}}+N_{M^{2+}}=28\end{matrix}\right.\left(1\right)\)
Lại có: \(\left\{{}\begin{matrix}A_{X^{2-}}-A_{M^{2+}}=8\\S_{X^{2-}}-S_{M^{2+}}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(Z_{X^{2-}}+N_{X^{2-}}\right)-\left(Z_{M^{2+}}+N_{M^{2+}}\right)=8\\\left(2Z_{X^{2-}}+N_{X^{2-}}\right)-\left(2Z_{M^{2+}}+N_{M^{2+}}\right)=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(Z_{X^{2-}}-Z_{M^{2+}}\right)+\left(N_{X^{2-}}-N_{M^{2+}}\right)=8\\2\left(Z_{X^{2-}}-Z_{M^{2+}}\right)+\left(N_{X^{2-}}-N_{M^{2+}}\right)=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}Z_{X^{2-}}-Z_{M^{2+}}=8\\N_{X^{2-}}-N_{M^{2+}}=0\end{matrix}\right.\left(2\right)\)
Từ (1) và (2) ta có:\(\left\{{}\begin{matrix}N_{X^{2-}}+N_{M^{2+}}=28\\Z_{X^{2-}}+Z_{M^{2+}}=28\\N_{X^{2-}}-N_{M^{2+}}=0\\Z_{X^{2-}}-Z_{M^{2+}}=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}Z_{X^{2-}}=18\\N_{X^{2-}}=14\\Z_{M^{2+}}=10\\N_{M^{2+}}=14\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}Z_X=16\\N_X=16\\Z_M=12\\N_M=12\end{matrix}\right.\)
Vậy X là Lưu huỳnh, M là Magie => MX là MgS

Gọi số p,e,n trong của M và X lần lượt là p1,e1,n1 , p2,e2,n2
=> 2(p1+e1+n1) + ( p2+e2+n2)=140
Mà số p=số e
=> 2(2p1 + n1) + ( 2p2 + n2) = 140 <=> (4p1+2p2) + (2n1+n2)=140 (I)
Lại có : (4p1+2p2)-(2n1+n2)=44 (II)
Từ (I) và (II ) => \(\left\{{}\begin{matrix}4p1+2p2=92\left(1\right)\\2n1+n2=48\end{matrix}\right.\)
Lại có : (p1 + n1) - (p2+n2)=23 (III)
(2p1 + n1 -1) - (2p2+n2+2) =31 (IV)
Từ (III) và (IV) => \(\left\{{}\begin{matrix}p1-p2=11\left(2\right)\\n1-n2=12\end{matrix}\right.\)
Từ (1) và (2) => \(\left\{{}\begin{matrix}p1=19\\p2=8\end{matrix}\right.\)
=> số e của M là 19 e
số e của X là 8 e
=> cấu hình e của M là : 1s22s22p63s23p64s1
cấu hình e của X là : 1s22s22p4

MX: \(\left\{{}\begin{matrix}2Z+N=84\\2Z-N=28\end{matrix}\right.\)⇔ \(\left\{{}\begin{matrix}Z=28\\N=28\end{matrix}\right.\)
⇒\(Z_M+Z_X=28\left(1\right)\)
Ta có : \(2Z_M-2-2Z_X-2=20\)
⇔ \(2Z_M-2Z_X=24\) (2)
Từ (1) và (2)⇒ \(\left\{{}\begin{matrix}Z_M+Z_X=28\\2Z_M-2Z_X=24\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}Z_M=20\\Z_X=8\end{matrix}\right.\)
⇒ M là Canxi , X là Oxi
⇒ \(A_M\)= 40 , \(A_X\)= 16
Vậy công thức phân tử của A là CaO

( 1 )
( 2 )
( 3 )
( 4 )
Từ (1) + (2) suy ra
(*)
Từ (3) và (4) suy ra
( ** )
Từ (* ) và ( ** )
--> --> m = Mg
--> Cl
MX2 = MgCl2