Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)

Đáp án D
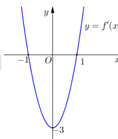
Dựa vào đồ thị hàm số y = f ' ( x ) ⇒ f ' x = 3 x 2 - 1
Khi đó f x = ∫ f ' x d x = x 3 - 3 x + C .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
f x = 4 f x = 0 ⇒ x 3 - 3 x + C = 4 3 x 2 - 1 = 0 ⇔ x = - 1 C = 2 (Do x < 0 suy ra f x = x 3 - 3 x + 2 C
Cho C ∩ O x ⇒ hoành độ các giao điểm là x = -2,x = 1
Khi đó S = ∫ - 2 1 x 3 - 3 x + 2 d x = 27 4 .

b: Thay x=2 vào (P), ta được:
\(y=-\dfrac{1}{4}\cdot2^2=-1\)
Vì (d) đi qua O(0;0) và A(2;-1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=0\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=0\end{matrix}\right.\)

Đáp án C
Số giao điểm với trục hoành là số nghiệm của phương trình
![]()


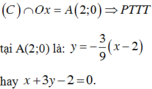

 Tính diện tích S của hình phẳng giới hạn bởi đồ thị
Tính diện tích S của hình phẳng giới hạn bởi đồ thị 



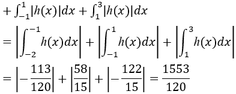


Đáp án C
Hoành độ giao điểm của đồ thị hàm số y = x 4 - 3 x 2 - 4 với trục hoành là nghiệm của phương trình