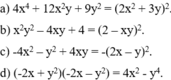
a)
4...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. Trả lời: a, \(-xy.\left(x^2+2xy-3\right)=-x^3y-2x^2y^2+3xy\) b, \(\left(12x^6y^5-3x^3y^4+4x^2y\right):6x^2y\) \(=12x^6y^5:6x^2y^2-3x^3y^4:6x^2y+4x^2y+6x^2y\) \(=2x^4y^3-\frac{1}{2}xy^3+\frac{2}{3}\) a.\(\left(-xy\right)\left(x^2+2xy-3\right)=-x^3y-2x^2y^2+6xy\) b.\(\left(12x^6y^5-3x^3y^4+4x^2y\right):6x^2y=2x^4y^4-\frac{1}{2}xy^3+\frac{2}{3}\) Ý 3 bạn bỏ dòng áp dụng....ta có nhé \(a^2+b^2+c^2+d^2\ge a\left(b+c+d\right)\) \(\Leftrightarrow\left(\frac{a^2}{4}-2.\frac{a}{2}b+b^2\right)+\left(\frac{a^2}{4}-2.\frac{a}{2}c+c^2\right)+\)\(\left(\frac{a^2}{4}-2.\frac{a}{d}d+d^2\right)+\frac{a^2}{4}\ge0\forall a;b;c;d\) \(\Leftrightarrow\left(\frac{a}{2}-b\right)+\left(\frac{a}{2}-c\right)+\)\(\left(\frac{a}{2}-d\right)^2+\frac{a^2}{4}\ge0\forall a;b;c;d\)( luôn đúng ) Dấu " = " xảy ra <=> a=b=c=d=0 6) Sai đề Sửa thành:\(x^2-4x+5>0\) \(\Leftrightarrow\left(x-2\right)^2+1>0\) 7) Áp dụng BĐT AM-GM ta có: \(a+b\ge2.\sqrt{ab}\) Dấu " = " xảy ra <=> a=b \(\Leftrightarrow\frac{ab}{a+b}\le\frac{ab}{2.\sqrt{ab}}=\frac{\sqrt{ab}}{2}\) Chứng minh tương tự ta có: \(\frac{cb}{c+b}\le\frac{cb}{2.\sqrt{cb}}=\frac{\sqrt{cb}}{2}\) \(\frac{ca}{c+a}\le\frac{ca}{2.\sqrt{ca}}=\frac{\sqrt{ca}}{2}\) Dấu " = " xảy ra <=> a=b=c Cộng vế với vế của các BĐT trên ta có: \(\frac{ab}{a+b}+\frac{bc}{b+c}+\frac{ca}{c+a}\le\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2}\) Áp dụng BĐT AM-GM ta có: \(\frac{ab}{a+b}+\frac{bc}{b+c}+\frac{ca}{c+a}\le\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2}\le\frac{\frac{a+b}{2}+\frac{b+c}{2}+\frac{c+a}{2}}{2}=\frac{2\left(a+b+c\right)}{4}=\frac{a+b+c}{2}\) Dấu " = " xảy ra <=> a=b=c 1)\(x^3+y^3\ge x^2y+xy^2\) \(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)\ge xy\left(x+y\right)\) \(\Leftrightarrow x^2-xy+y^2\ge xy\) ( vì x;y\(\ge0\)) \(\Leftrightarrow x^2-2xy+y^2\ge0\) \(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng ) \(\Rightarrow x^3+y^3\ge x^2y+xy^2\) Dấu " = " xảy ra <=> x=y 2) \(x^4+y^4\ge x^3y+xy^3\) \(\Leftrightarrow x^4-x^3y+y^4-xy^3\ge0\) \(\Leftrightarrow x^3\left(x-y\right)-y^3\left(x-y\right)\ge0\) \(\Leftrightarrow\left(x-y\right)^2\left(x^2+xy+y^2\right)\ge0\)( luôn đúng ) Dấu " = " xảy ra <=> x=y 3) Áp dụng BĐT AM-GM ta có: \(\left(a-1\right)^2\ge0\forall a\Leftrightarrow a^2-2a+1\ge0\)\(\forall a\Leftrightarrow\frac{a^2}{2}+\frac{1}{2}\ge a\forall a\) \(\left(b-1\right)^2\ge0\forall b\Leftrightarrow b^2-2b+1\ge0\)\(\forall b\Leftrightarrow\frac{b^2}{2}+\frac{1}{2}\ge b\forall b\) \(\left(a-b\right)^2\ge0\forall a;b\Leftrightarrow a^2-2ab+b^2\ge0\)\(\forall a;b\Leftrightarrow\frac{a^2}{2}+\frac{b^2}{2}\ge ab\forall a;b\) Cộng vế với vế của các bất đẳng thức trên ta được: \(a^2+b^2+1\ge ab+a+b\) Dấu " = " xảy ra <=> a=b=1 4) \(a^2+b^2+c^2+\frac{3}{4}\ge a+b+c\) \(\Leftrightarrow\left[a^2-2.a.\frac{1}{2}+\left(\frac{1}{2}\right)^2\right]\)\(+\left[b^2-2.b.\frac{1}{2}+\left(\frac{1}{2}\right)^2\right]\)\(+\left[c^2-2.c.\frac{1}{2}+\left(\frac{1}{2}\right)^2\right]\ge0\forall a;b;c\) \(\Leftrightarrow\left(a-\frac{1}{2}\right)^2\)\(+\left(b-\frac{1}{2}\right)^2\)\(+\left(c-\frac{1}{2}\right)^2\ge0\forall a;b;c\)( luôn đúng) Dấu " = " xảy ra <=> a=b=c=1/2 Câu hỏi của Fire Sky - Toán lớp 8 - Học toán với Em tham khảo tại link này nhé! \(1,\left(x+y\right)\left(x^2-xy+y^2\right)\ge xy\left(x+y\right)\Leftrightarrow x^2-2xy+y^2\ge0\)) Bài 1: a) \(\frac{4}{9}x^2-y^2=\left(\frac{2}{3}x-y\right)\left(\frac{2}{3}x+y\right)\) b) \(x^2-5=\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)\) c) \(4x^2+6x+9=\left(2x+2\right)^2+5\)ko hiểu ??? d) \(\frac{1}{9}x^2-\frac{4}{3}xy+4=\left(\frac{1}{3}x\right)^2-2.\frac{1}{3}x.2+2^2=\left(\frac{1}{3}x-2\right)^2\) Bài 2: a) \(\left(\frac{1}{2}x-\frac{1}{3}y\right)\left(\frac{1}{2}x+\frac{1}{3}y\right)=\frac{1}{4}x^2-\frac{1}{9}y^2\) b) \(\left(2x-\frac{1}{3}y\right)\left(4x^2+\frac{2}{3}xy+\frac{1}{9}x^2\right)=8x^3-\frac{1}{27}y^3\) c) \(\left(3x-5y\right)\left(9x^2+15xy+\frac{1}{9}x^2\right)=27x^3-125y^3\)
K
Khách
CM
Cao Minh Tâm
15 tháng 3 2019
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QA
24 tháng 8 2021
NM
Nguyễn Minh Quang
Giáo viên
24 tháng 8 2021
21 tháng 3 2019
21 tháng 3 2019
24 tháng 3 2019
LG
21 tháng 3 2019
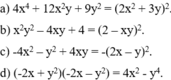
\(\Leftrightarrow\left(x+y\right)^2\ge o\)
16 tháng 7 2019
16 tháng 7 2019
