Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

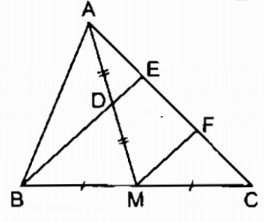
Gọi F là trung điểm của EC
Trong ∆ CBE ta có:
M là trung điểm của cạnh CB
F là trung điểm của cạnh CE
Nên MF là đường trung bình của ∆ CBE
⇒ MF // BE (tính chất đường trung bình của tam giác)
Hay DE // MF
Trong tam giác AMF ta có:
D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF=FC=\(\dfrac{EC}{2}\) nên AE=\(\dfrac{EC}{2}\)

a: Gọi K là trung điểm của NC
=>AN=NK=KC
Xét ΔBNC có
M,K lần lượt là trung điểm của CB và CN
nên MK là đường trung bình
=>MK//BN và MK=1/2BN
Xét ΔAMK có
N là trung điểm của AK
NI//MK
Do đó: I là trung điểm của AM
b: Xét ΔAMK có IN//MK
nên IN/MK=AN/AK=1/2
=>IN=1/2MK=1/2x1/2BN=1/4BN
=>IN=1/3BI
c: Gọi D là trung điểm của BE
=>AE=ED=BD
Xét ΔBEC có
M,D lần lượt là trung điểm của BC,BE
nên MD là đường trung bình
=>MD//EC
Xét ΔADM cso
I,E lần lượt là trung điểm của AM và AD
nen IE là đường trung bình
=>IE//MD
=>IE//EC
=>C,I,E thẳng hàng
a: Gọi K là trung điểm của NC
=>AN=NK=KC
Xét ΔBNC có
M,K lần lượt là trung điểm của CB và CN
nên MK là đường trung bình
=>MK//BN và MK=1/2BN
Xét ΔAMK có
N là trung điểm của AK
NI//MK
Do đó: I là trung điểm của AM
b: Xét ΔAMK có IN//MK
nên IN/MK=AN/AK=1/2
=>IN=1/2MK=1/2x1/2BN=1/4BN
=>IN=1/3BI
c: Gọi D là trung điểm của BE
=>AE=ED=BD
Xét ΔBEC có
M,D lần lượt là trung điểm của BC,BE
nên MD là đường trung bình
=>MD//EC
Xét ΔADM cso
I,E lần lượt là trung điểm của AM và AD
nen IE là đường trung bình
=>IE//MD
=>IE//EC
=>C,I,E thẳng hàng

a)Ta có: BM=MC; AN=NC
=>MN là đường trung bình của ΔABC
=>MN//AB
Mà ∠BAC đồng vị với ∠MNC nên ∠BAC=∠MNC=90*
Hay MN ⊥AC
b) Ta có : MN⊥AC(câu a)
=> Mn là đường cao của ΔAMC
Mà AN=MC=> đường cao cũng là đường trung tuyến
Hay ΔAMC cân tại M
c) Ta có: AM là đường trung tuyến của ΔABC
=>BM=MC.
Ta lại có MC=BM=1/2BC=>BC=2MC
Mà MC=AM(do ΔAMC cân tại A)=>BC=2AM

Ta gọi E là trung điểm của DC
Vì tam giác ABC có
BM = MC
DE = EC
=> BD // ME
=> DI // ME
mà tâm giac ADE có AD = DE và DI // ME nên AI = IM (đpcm)

Bài 1:
Gọi G là trung điểm của BK
Xét ΔBKC có
M là trung điểm của BC
G là trung điểm của BK
Do đó; MG là đường trung bình
=>MG//KC
hay KI//GM
Xét ΔAGM có
I là trung điểm của AM
IK//GM
Do đó; K là trung điểm của AG
=>AK=KG=GB
=>AK=1/3AB

