Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

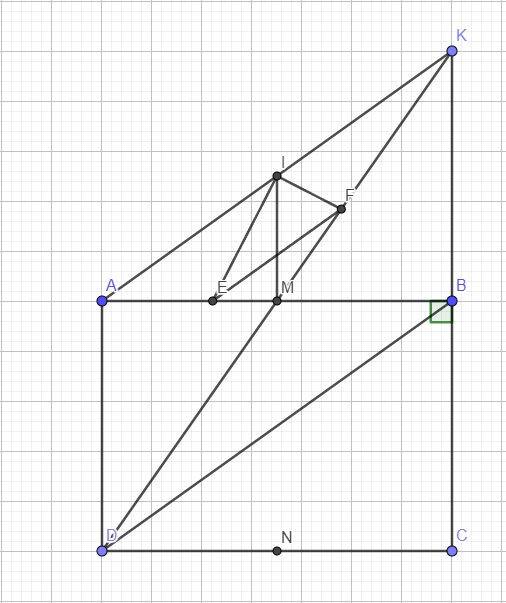
a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD

a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)

AC=AD
OC=OD
=>AO là trung trực của CD
=>OA vuông góc CD tại I
góc AMB=1/2*180=90 độ
góc KMB+góc KIB=180 độ
=>KMBI nội tiếp

A B C O F H E D I K A' C' B' M N
a) Do BHCK là hình bình hành nên BH // KC \(\Rightarrow KC\perp AC\Rightarrow\widehat{ACK}=90^o\)
KB // CF \(\Rightarrow\widehat{ABK}=90^o\)
Hai tam giác vuông ABK và ACK chung cạnh huyền AK nên A, B, C, K cùng thuộc đường tròn đường kính AK. Vậy K thuộc đường tròn (O).
b) Do BHCK là hình bình hành nên I là trung điểm HK.
AK là đường kính nên \(\widehat{AA'K}=90^o\Rightarrow\) DI // A'K
Vậy DI là đường trung bình tam giác HA'K. Suy ra HD = DA'
Tương tự : HF = FC' ; HE = EB'
Ta có : \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=\frac{AD+DA'}{AD}+\frac{BE+EE'}{BE}+\frac{CF+FC'}{CF}\)
\(=1+\frac{DA'}{AD}+1+\frac{EB'}{BE}+1+\frac{FC'}{CF}=3+\left(\frac{DA'}{AD}+\frac{EB'}{BE}+\frac{FC'}{CF}\right)\)
\(=3+\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)=3+\left(\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}\right)\)
\(=3+\frac{S_{ABC}}{S_{ABC}}=3+1=4\)
Vậy nên \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=4\)
c) Ta thấy \(\widehat{AKC}=\widehat{ABC}=\widehat{AHF}\)
Vậy nên \(\Delta AFH\sim\Delta ACK\left(g-g\right)\Rightarrow\frac{AH}{AK}=\frac{AF}{AC}\) (1)
AFH và AEH là các tam giác vuông chung cạnh huyền AH nên AFHE là tứ giác nội tiếp.
Vậy thì \(\widehat{AFM}=\widehat{AHE}=\widehat{ACN}\)
Lại có \(\Delta AFH\sim\Delta ACK\Rightarrow\widehat{FAM}=\widehat{CAN}\)
Nên \(\Delta AFM\sim\Delta ACN\left(g-g\right)\Rightarrow\frac{AF}{AC}=\frac{AM}{AN}\) (2)
Từ (1) và (2) suy ra \(\frac{AH}{AK}=\frac{AM}{AN}\Rightarrow\frac{AH}{AM}=\frac{AK}{AN}\Rightarrow\) MN // HK (Định lý Talet đảo)

B C M E D 1 2 3 4 A N 1 2 1 2 1 2 1 2 1 2 I
tg là tam giác nha !
a )
Ta có : gócA1 + gócBAC = gócDAC ( AB nằm giữa AD và AC )
=> gócA1 = gócDAC - gócBAC = 90o - gócBAC ( 1 )
Ta có : gócA2 + gócBAC = gócBAE ( AC nằm giữa AB và AE )
=> gócA2 = gócBAE - gócBAC = 90o - gócBAC ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : gócA1 = gócA2 .
Xét tgABD và tgACE , có :
AD = AC ( gt )
AB = AE ( gt )
gócA1 = gócA2 ( cmt )
Do đó : tgABD = tgACE ( c - g - c )
=> BD = CE ( 2 cạnh tương ứng ) .
b ) Xét tgABM và tgNCM , có :
gócM1 = gócM2
BM = CM ( AM là trung tuyến)
AM = NM ( gt )
Do đó : tgABM = tgNCM ( c - g - c )
=> gócC1 = gócB1 ( 2 góc tương ứng )
Mà : gócB1 = gócADC + gócA1 ( góc ngoài của tg bằng tổng 2 góc trong không kề với nó )
Do đó : gócC1 = gócADC + gócA1
Ta có : gócC2 + gócDAC + gócADC = 180o ( tổng 3 góc trong tg )
=> gócC2 = 180o - gócDAC - gócADC = 180o - 90o - gócADC = 90o - gócADC
Ta có : gócACN = gócC1 + gócC2 ( DC nằm giữa AC và NC )
=> gócACN = ( gócADC + gócA1 ) + ( 90o - gócADC ) = gócADC + gócA1 + 90o - gócADC = 90o + gócA1 ( 3 )
Ta có : gócDAE = gócBAE + gócA1 ( AB nằm giữa AD và AE )
=> gócDAE = 90o + gócA1 ( 4 )
Từ ( 3 ) và ( 4 ) suy ra : gócACN = gócDAE ( 5 )
Ta có : tgABM = tgNCM ( cmt )
=> AB = CN ( 2 cạnh tương ứng )
Mà : AB = AE ( gt )
Do đó : CN = AE ( 6 )
Xét tgADE và tgACN , có :
AD = AC ( gt )
AE = CN ( cmt ( 6 ) )
gócACN = gócDAE ( cmt ( 5 ) )
Do đó : tgADE = tgACN ( c - g - c )
c ) Nằm ngoài khả năng của mình rồi !
Học tốt nha !