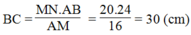Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K H I
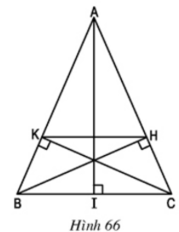
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
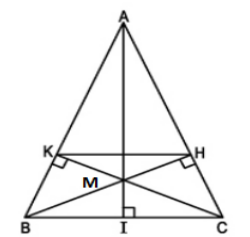
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

Hình bạn tự vẽ nhé
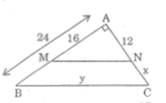
Áp dụng định lý Pi-ta-go vào tam giác AMN vuông tại A ta được:
\(AM^2+AN^2=MN^2\)
\(400=MN^2\)
\(\Rightarrow MN=20\)
Xét tam giác AMN có BC//MN
\(\Rightarrow\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)( Hệ qua của định lý Ta-let)
\(\Rightarrow\frac{2}{3}=\frac{20}{BC}=\frac{12}{AC}\)
\(\Rightarrow\hept{\begin{cases}BC=30\left(cm\right)\\AC=18\left(cm\right)\end{cases}}\)
Ta có: AN+NC=AC ( h.vẽ)
\(\Rightarrow NC=6\)(cm)
Vậy ...


a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou

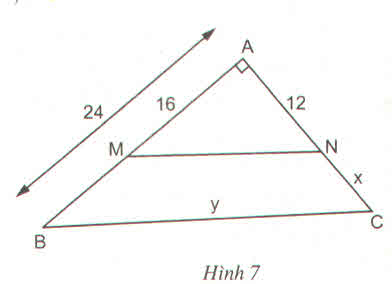





Trong ΔABC, ta có: MN // BC (gt)
Suy ra: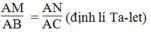
Suy ra: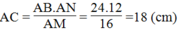
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:
Vậy: