NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
F
9 tháng 3 2020
a) d là đường trung trực của BC nên B và C đối xứng qua d D đối xứng với A qua d nên đường thẳng đối xứng với AB qua d là DC do AB và CD đối xứng qua d nên AC=CD.
c) ta có đoạn thẳng đối xứng với AC qua d là DB vì d là đường trung trực của AD và BC nên AD vuông góc với d và BC vuông với d vậy AD//BC, do đó ABCD là hình thanh do AC đối xứng với BD qua d nên AC=DB vậy hình thanh ABCD có hai đường chéo bằng nhau nên là hình thang cân
Câu b mk ko bt nha
17 tháng 5 2018
a) xét tam giác HBA và tam giác ABC có:
Góc BHA = góc BAC
Chung góc ABC
=) Tam giác HBA đồng dạng với tam giác ABC (g-g)
b) Áp dụng định lý py-ta-go cho tam giác ABC vuông tại A ta đươc:
AB^2 + AC^2 = BC^2
(=) 9^2 + 12^2 = BC^2
(=) BC = 15
do tam giác HBA đồng dạng với tam giác ABC
=) BA/BC = HA/AC
(=) 9/15 = HA/12
(=) HA = 7,2
HV
3
F
29 tháng 9 2017
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)
29 tháng 9 2017
Bạn chỉ việc nối B vs D hoặc A vs C
Sau đó CM 2 cạnh đối song song và bằng nhau
Dựa vào tính chất đường trung bình
24 tháng 6 2016
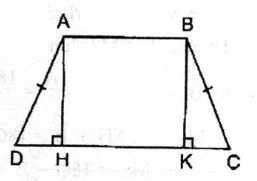
Xét tam giác AHD vuông tại H và tam giác BKC vuông tại K
Ta có: AD= BC (gt)
Góc D = góc C
=> tam giác AHD= tam giác BKC (cạnh huyền- góc nhọn)
=> DH= CK ( 2 cạnh tương ứng)
24 tháng 6 2016
xét tam giác AHD và tam giác BKC có:
AD = BC (gt)
góc ADH = góc BCK (gt)
góc AHD = góc AKC = 900
=> tam giác ... = tam giác .... (ch-gn)
=> DH = CK (cạnh tương ứng)
t i c k nha!! 463745768658897697696789768568654
16 tháng 6 2019
A B D C H K
Có hình thang ABCD cân
⇒AD=BC ; ∠ADC=∠BCD
Có AH⊥DC
⇒∠AHD=∠AHC
Có BK⊥DC
⇒∠BKC=∠BKD
* Xét △AHD(∠AHD=90) và ΔBKC(∠BKC=90) có
AD=BC(c/m trên)
∠ADH=∠BCK
⇒△AHD=ΔBKC( cạnh huyền-góc nhọn)
⇒DH=KC(2 cạnh tương ứng)(đpcm)
Tranh đây ...