

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔAOB đồng dạng với ΔCOD
=>\(k=\dfrac{AB}{CD}=\dfrac{10}{25}=\dfrac{2}{5}\)

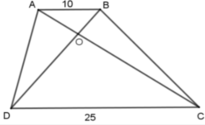
AB // CD nên ΔAOB ⁓ ΔCOD.
Tỉ số đồng dạng
A O O C = B O O D = A B C D = 10 25 = 2 5
Đáp án: C

BẠN DÙNG ĐỊNH LÝ TA-LÉT ĐỂ C/M OM=ON
Vì OM // AB & OM // CD nên
\(\frac{OM}{AB}=\frac{DM}{AD}\&\frac{OM}{CD}=\frac{AM}{AD}\)
\(\Rightarrow\frac{OM}{AB}+\frac{OM}{CD}=\frac{DM}{AD}+\frac{AM}{AD}\)
\(\Leftrightarrow OM\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{DM+AM}{AD}\)
\(\Leftrightarrow\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OM}\)(1)
TƯƠNG TỰ \(\frac{1}{AB}+\frac{1}{CB}=\frac{1}{ON}\)(2)
CỘNG VẾ VỚI VẾ CỦA (1) VÀ (2) TA CÓ:
\(2\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{1}{OM}+\frac{1}{ON}\)MÀ OM=ON(C/M TRÊN) NÊN MN=2.OM
\(\Rightarrow2\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{1}{OM}+\frac{1}{OM}=\frac{2}{OM}\)
\(\Leftrightarrow\frac{1}{AB}+\frac{1}{CD}=\frac{2}{2.OM}=\frac{2}{MN}\left(ĐPCM\right)\)

tham khảo :
https://lazi.vn/edu/exercise/582904/cho-hinh-thang-abcd-ab-cd-cheo-cat-nhau-tai-o-p

Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:
Suy ra ![]() (hệ quả định lí ta-lét)
(hệ quả định lí ta-lét)
Vậy OA.OD = OB.OC