Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có diện tích ABCD =31,2 cm^2 suy ra AB=BC=6,5 cm .... AD=BC=4,8cm
Xét tam giác ABC vuông tại B (ABCD là hình chữ nhật)
suy ra: AC^2 = AB^2+BC^2 (định lí py ta go)
hay: AC^2=65,29
AC= căn 65,29 cm.

1. Áp dụng định lý Pi-ta-go ta có:
\(AB^2+BC^2=AC^2\Rightarrow BC=\sqrt{10^2-8^2}=6cm\)
Diện tích hình chữ nhật là:\(AB.BC=8.6=48cm^2\)
2.B

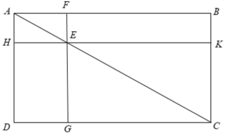
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
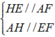 ⇒ AFEH là hình bình hành.
⇒ AFEH là hình bình hành.


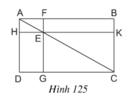
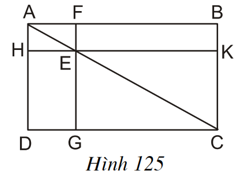
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.

Bài này mà của lớp 9 thì dễ, lớp 8 thì làm thế này nhé.
Trên AD lấy điểm E sao cho góc ABE=60 độ.
Đặt AB = x (x>0)
Tam giác ABE vuông có góc ABE = 60 độ nên BE = 2 AB = 2x.
Áp dụng định lí Pi-ta-go => AE= \(\sqrt{3}\)x
Tam giác BED cân tại E => BE = ED = 2x.
=> AD = AE + ED =\(\sqrt{3}\)x +2x =x(\(\sqrt{3}\) +2)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD
BD2 = AB2 + AD2 <=> 172 = x2 +(\(\sqrt{3}\)+2)2 x2 => x=\(\frac{17}{\sqrt{8+4\sqrt{3}}}\)
=> AB, AD => Diện tích của hcn ABCD.