Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để tính tốc độ chuyển động trong 25s đầu, chúng ta cần biết độ dịch chuyển trong khoảng thời gian đó. Từ đồ thị, chúng ta có thể thấy rằng độ dịch chuyển trong 25s đầu là khoảng 40m. Vì vậy, tốc độ chuyển động trong 25s đầu là:
tốc độ = độ dịch chuyển / thời gian = 40m / 25s = 1.6 m/s
b) Để xác định chiều và tốc độ chuyển động từ t = 35s đến t = 60s, chúng ta cần xem xét đường cong đồ thị trong khoảng thời gian này. Nếu đường cong đồ thị nằm trên trục dương, người đó đang bơi về phía dương, và nếu nằm trên trục âm, người đó đang bơi về phía âm.
Trong trường hợp này, chúng ta không có thông tin cụ thể về đồ thị. Vì vậy, không thể xác định được chiều di chuyển.
c) Để tính độ dịch chuyển trong cả quá trình bơi, chúng ta cần tính tổng diện tích dưới đường cong đồ thị trong khoảng thời gian từ t = 0s đến t = 60s. Khi đó, diện tích dưới đường cong đồ thị sẽ tương đương với độ dịch chuyển.
Tuy nhiên, vì chúng ta không có đồ thị cụ thể, không thể tính được độ dịch chuyển trong cả quá trình bơi.
\(a,\) Gọi điểm tại \(t=25s\) là H.
Tốc độ chuyển động trong 25s đầu là :
\(v_A=\left|+\dfrac{AH}{OH}\right|=\left|\dfrac{50}{25}\right|=2m/s\)
\(b,t=35s\rightarrow t=60s\) : người đó bơi theo chiều âm \(\left(-\right)\) (Do đường thẳng trên đồ thị đi xuống).
\(v=\left|\dfrac{d}{\Delta t}\right|=\left|-\dfrac{50}{60-35}\right|=\left|-2\right|=2m/s\)
\(c,\) Quá trình bơi được chia thành 3 lần khác nhau theo đồ thị biểu diễn :
+ Lần 1 : Từ \(0s\rightarrow25s\) : theo chiều dương \(\left(+\right)\) nên ta có tốc độ dịch chuyển lúc này chính là \(v_A=2m/s\)
+ Lần 2: Từ \(25s\rightarrow35s\) : người đó đứng yên nên tốc độ dịch chuyển lúc này \(=0\).
+ Lần 3 : Từ \(35s\rightarrow60s\) : theo chiều âm \(\left(-\right)\) nên ta có tốc độ dịch chuyển lúc này chính là \(v=2m/s\)
Vậy tốc độ dịch chuyển trong cả quá trình bơi là : \(2+0+2=4m/s\).

Từ giây 45 đến giây 60, ta có t = 60 - 45 = 15 (s)
Người đó không đổi chiều chuyển động từ giây 45 đến 60 nên ta có:
s = d = 40 - 25 = 15 (m).
=> Vận tốc (tốc độ) của người bơi là: \(v = \frac{d}{t} = \frac{{15}}{{15}} = 1(m/s)\).

Chọn đáp án A
? Lời giải:
+ Giả sử người này bơi từ A đến B rồi quay lại về A. Chọn chiều dương từ A đến B, gốc tọa độ và gốc thời gian tại A. Trong suốt quãng đường đi và về, độ dời: Δx = x2 – x1
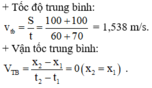

Chọn A.
Độ lớn vận tốc của người đối với bờ khi bơi ngược chiều và bơi xuôi chiều lần lượt là:


Để tính vận tốc trung bình, ta sử dụng công thức:
Vận tốc trung bình = Quãng đường / Thời gian
a) Trong lần bơi đầu tiên theo chiều dài bể bơi:
Quãng đường: 50m Thời gian: 20s
Vận tốc trung bình = 50m / 20s = 2.5 m/s
Vậy vận tốc trung bình trong lần bơi đầu tiên theo chiều dài bể bơi là 2.5 m/s.
b) Trong lần bơi về:
Quãng đường: 50m Thời gian: 22s
Vận tốc trung bình = 50m / 22s ≈ 2.27 m/s
Vậy vận tốc trung bình trong lần bơi về là khoảng 2.27 m/s.
c) Trong suốt quãng đường bơi đi và về:
Quãng đường đi + quãng đường về = 50m + 50m = 100m Thời gian đi + thời gian về = 20s + 22s = 42s
Vận tốc trung bình = 100m / 42s ≈ 2.38 m/s



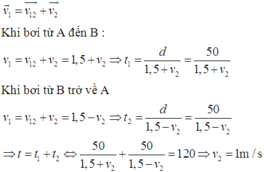
1.
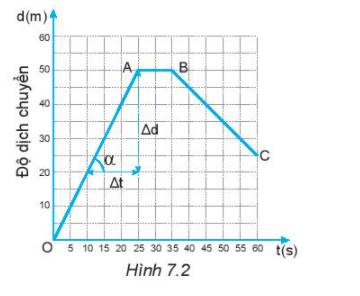
Từ đồ thị ta thấy, trong 25s đầu người đó chuyển động thẳng từ O – A và không đổi chiều, độ dịch chuyển trong 25 s đầu là 50 m.
Suy ra: Mỗi giây người đó bơi được: \(\frac{{50}}{{25}} = 2\left( m \right)\)
Vận tốc của người đó là: \(v = \frac{d}{t} = \frac{{50}}{{25}} = 2\left( {m/s} \right)\)
2.
Từ A – B: người đó không bơi => Người đó không bơi từ giây 25 đến giây 35.