
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x là ƯC của n+3 và 2n+5
=> x là ƯC của 2(n+3)=2n+6 và 2n+5
=> x là Ư của (2n+6)-(2n+5) = 2n+6-2n-5=1
=> x=1
Vậy ƯC(n+3;2n+5)=1
học tốt

\(\frac{5.4^{15}.9^8-4.3^{17}.8^9}{5.2^{11}.6^{18}-7.2^{28}.27^6}\)\(=\frac{5.\left(2^2\right)^{15}.\left(3^2\right)^8-\left(2^2\right).3^{17}.\left(2^3\right)^9}{5.2^{11}.\left(2.3\right)^{18}-7.2^{28}.\left(3^3\right)^6}\)\(=\frac{5.2^{30}.3^{16}-2^2.3^{17}.2^{27}}{5.2^{11}.2^{18}.3^{18}-7.2^{28}.3^{18}}\)
\(=\frac{5.2^{30}.3^{16}-2^{29}.3^{17}}{5.2^{29}.3^{18}-7.2^{28}.3^{18}}=\frac{2^{28}.3^{16}.\left(5.2^2-2.3\right)}{2^{28}.3^{16}.\left(5.2.3^2-7.3^2\right)}\)
\(=\frac{5.2^2-2.3}{5.2.3^2-7.3^2}=\frac{5.4-6}{5.2.9-7.9}=\frac{20-6}{90-63}\)
\(=\frac{14}{27}\)
\(\frac{5.4^{15}.9^8-4.3^{17}.8^9}{5.2^{11}.6^{18}-7.2^{28}.27^6}=\frac{5.\left(2^2\right)^{15}.\left(3^2\right)^8-2^2.3^{17}.\left(2^3\right)^9}{5.2^{11}.\left(2.3\right)^{18}-7.2^{28}.\left(3^3\right)^6}\)\(=\frac{5.2^{30}.3^{16}-2^2.3^{17}.2^{27}}{5.2^{11}.2^{18}.3^{18}-7.2^{28}.3^{18}}=\frac{5.2^{30}.3^{16}-2^{29}.3^{17}}{5.2^{29}.3^{18}-7.2^{28}.3^{18}}\)\(=\frac{2^{29}.3^{16}.\left(5+2-3\right)}{2^{28}.3^{18}.\left(5+2\right)}\)\(=\frac{2.4}{3^2.7}=\frac{8}{63}\)

\(\dfrac{x-2}{3}=\dfrac{x+1}{4}\)
\(4\left(x-2\right)=3\left(x+1\right)\)
\(4x-8=3x+3\)
\(x=11\)

4/
a. $101+254=355$
b. $(-35)+(-67)=-(35+67)=-102$
c. $51+(-97)=-(97-51)=-46$
d. $(-175)+56=-(175-76)=-99$
e. $195-55=140$
f. $1650-(-150)=1650+150=1800$
g.
$(-101)-(-35)=-101+35=-(101-35)=-66$
h.
$=173+(-173)+(62+38)=0+100=100$
i.
$=-(154+46)+(132+68)=-200+200=0$
k.
$(-2023)-(-2023+89)=-2023+2023-89=0-89=-89$
l.
$=365+143-143-365=(365-365)+(143-143)=0+0=0$
m.
$=64-35+45-64-45=(64-64)+(45-45)-35=0+0-35=-35$

Ta có: 5+5\(^2\)+5\(^3\)+5\(^4\)+....+5\(^{60}\)= (5+5\(^2\))+(5\(^3\)+5\(^4\) ) +....+( 5\(^{59}\)+5\(^{60}\))=
= 30+ 5^2.(5+5^2)+...+5^58.(5+5^2)= 30+5^2.30+...+5^58.30= 30.(1+5^2+...+5^58)
Vì 30 \(⋮\)6 \(\Rightarrow\)30.(1+5^2+...+5^58) \(⋮\)6 hay 5+5\(^2\)+5\(^3\)+5\(^4\)+....+5\(^{60}\)\(⋮\)6
5+5\(^2\)+5\(^3\)+5\(^4\)+....+5\(^{60}\)= (5+5\(^2\)+5\(^3\) ) +(5\(^4\) + 5^5+5^6) +....+( 5^58+5\(^{59}\)+5\(^{60}\))=
= 155+ 5^3.(5+5^2+5^3)+...+5^57.(5+5^2+5^3)= 155+5^3.155+...+5^57.155=155.(1+5^3+...+5^57)
Vì 155 \(⋮\) 31 \(\Rightarrow\) 155.(1+5^3+...+5^57) \(⋮\) 31 hay 5+5\(^2\)+5\(^3\)+5\(^4\)+....+5\(^{60}\)\(⋮\) 31
Bạn vào chỗ câu hỏi của bạn Trương NGuyễn Ngọc Mỹ, giải tương tự giống bài của mình nhé

Đặt \(A=1+3+3^2+3^3+...+3^{2017}\)
\(3A=3\left(1+3+3^2+3^3+...+3^{2017}\right)\)
\(=3+3^2+3^3+3^4+...+3^{2018}\)\(3A-A=\left(3+3^2+3^3+3^4+...+3^{2018}\right)-\left(1+3+3^2+3^3+...+3^{2017}\right)\)\(2A=3^{2018}-1\Rightarrow A=\frac{3^{2018}-1}{2}\)
Vậy \(A=\frac{3^{2018}-1}{2}\)
gọi bieu thuc tren la A
A= 1+3+3^2+..+3^2017
3A= 3.(1+3+362+..+3^2017)
3A=3+3^2+3^3+...+3^2018
3A - A= (3+ 3^2+3^3+...+3^2018) - (1+3+3^2+...+3^2017)
2A= 3^2018 - 1
=> A= \(\frac{3^{2018}-1}{2}\)

S = 1 + 4 + 7 + ... + 79 ( cách đều 3 đơn vị )
Dãy có số số hạng là : ( 79 - 1 ) : 3 + 1 = 27 ( số )
=> S = 1 + 4 + 7 + ... + 79 = ( 1 + 79 ) . 27 : 2 = 1080

\(20⋮x\Rightarrow x\inƯ\left(20\right)=\left\{1;2;4;5;10;20\right\}\)
Vậy \(x\in\left\{1;2;4;5;10;20\right\}\)
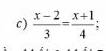 giúp mik với HELP ME
giúp mik với HELP ME
\(\frac{3}{4}+\frac{9}{5}\div\frac{3}{2}-1\)
\(=\frac{3}{4}+\frac{9}{5}\times\frac{2}{3}-1\)
\(=\frac{3}{4}+\frac{6}{5}-1\)
\(=\frac{15}{20}+\frac{24}{20}-1\)
\(=\frac{39}{20}-1\)
\(=\frac{39}{20}-\frac{20}{20}\)
\(=\frac{19}{20}\)
đây là toán lớp 4 mà
a) \(\frac{3}{4}+\frac{9}{5}\div\frac{3}{2}-1\)
\(=\frac{3}{4}+\frac{9}{5}.\frac{2}{3}-1\)
\(=\frac{3}{4}+\frac{6}{5}-1\)
\(=\frac{15}{20}+\frac{24}{20}-\frac{20}{20}\)
\(=\frac{19}{20}\)
@Lưu Xuân Phúc
Lớp 6 trước khi học ps thì ng ta cx cho ôn lại 1 chút phần ps lớp 4 mà bn.
HT