Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\int\dfrac{x^3dx}{\left(x^8-4\right)^2}\)
Đặt \(x^4=t\Rightarrow x^3dx=\dfrac{1}{4}dt\Rightarrow I=\dfrac{1}{4}\int\dfrac{dt}{\left(t^2-2\right)^2}=\dfrac{1}{4}\int\dfrac{dt}{\left(t-\sqrt{2}\right)^2\left(t+\sqrt{2}\right)^2}\)
\(=\dfrac{1}{32}\int\left(\dfrac{1}{t-\sqrt{2}}-\dfrac{1}{t+\sqrt{2}}\right)^2dt=\dfrac{1}{32}\int\left(\dfrac{1}{\left(t-\sqrt{2}\right)^2}+\dfrac{1}{\left(t+\sqrt{2}\right)^2}-\dfrac{2}{\left(t+\sqrt{2}\right)\left(t-\sqrt{2}\right)}\right)dt\)
\(=\dfrac{1}{32}\int\left(\dfrac{1}{\left(t-\sqrt{2}\right)^2}+\dfrac{1}{\left(t+\sqrt{2}\right)^2}-\dfrac{1}{\sqrt{2}}\left(\dfrac{1}{t-\sqrt{2}}-\dfrac{1}{t+\sqrt{2}}\right)\right)dt\)
\(=\dfrac{1}{32}\left(\dfrac{-1}{t-\sqrt{2}}-\dfrac{1}{t+\sqrt{2}}-\dfrac{1}{\sqrt{2}}ln\left|\dfrac{t-\sqrt{2}}{t+\sqrt{2}}\right|\right)+C\)
\(=\dfrac{1}{32}\left(\dfrac{-1}{x^4-\sqrt{2}}-\dfrac{1}{x^4+\sqrt{2}}-\dfrac{1}{\sqrt{2}}ln\left|\dfrac{x^4-\sqrt{2}}{x^4+\sqrt{2}}\right|\right)+C\)
2/ \(I=\int\dfrac{\left(2x+1\right)dx}{\left(x^2+x-1\right)\left(x^2+x+3\right)}=\dfrac{1}{4}\int\left(\dfrac{1}{x^2+x-1}-\dfrac{1}{x^2+x+3}\right)\left(2x+1\right)dx\)
\(=\dfrac{1}{4}\int\left(\dfrac{2x+1}{x^2+x-1}-\dfrac{2x+1}{x^2+x+3}\right)dx\)
\(=\dfrac{1}{4}\left(\int\dfrac{d\left(x^2+x-1\right)}{x^2+x-1}-\int\dfrac{d\left(x^2+x+3\right)}{x^2+x+3}\right)\)
\(=\dfrac{1}{4}ln\left|\dfrac{x^2+x-1}{x^2+x+3}\right|+C\)
3/ Đặt \(\sqrt[3]{x}=t\Rightarrow x=t^3\Rightarrow dx=3t^2dt\)
\(\Rightarrow I=\int\dfrac{3t^2.sint.dt}{t^2}=3\int sint.dt=-3cost+C=-3cos\left(\sqrt[3]{x}\right)+C\)
4/ \(I=\int\dfrac{dx}{1+cos^2x}=\int\dfrac{\dfrac{1}{cos^2x}dx}{\dfrac{1}{cos^2x}+1}\)
Đặt \(t=tanx\Rightarrow\left\{{}\begin{matrix}dt=\dfrac{1}{cos^2x}dx\\\dfrac{1}{cos^2x}=1+tan^2x=1+t^2\end{matrix}\right.\)
\(\Rightarrow I=\int\dfrac{dt}{1+t^2+1}=\int\dfrac{dt}{t^2+2}=\dfrac{1}{2}\int\dfrac{dt}{\left(\dfrac{t}{\sqrt{2}}\right)^2+1}\)
\(=\dfrac{1}{2}.\sqrt{2}.arctan\left(\dfrac{t}{\sqrt{2}}\right)+C=\dfrac{1}{\sqrt{2}}arctan\left(\dfrac{tanx}{\sqrt{2}}\right)+C\)
5/ \(I=\int\dfrac{sinx+cosx}{4+2sinx.cosx-sin^2x-cos^2x}dx=\int\dfrac{sinx+cosx}{4-\left(sinx-cosx\right)^2}dx\)
Đặt \(sinx-cosx=t\Rightarrow\left(cosx+sinx\right)dx=dt\)
\(\Rightarrow I=\int\dfrac{dt}{4-t^2}=-\int\dfrac{dt}{\left(t-2\right)\left(t+2\right)}=\dfrac{1}{4}\int\left(\dfrac{1}{t+2}-\dfrac{1}{t-2}\right)dt\)
\(=\dfrac{1}{4}ln\left|\dfrac{t+2}{t-2}\right|+C=\dfrac{1}{4}ln\left|\dfrac{sinx-cosx+2}{sinx-cosx-2}\right|+C\)
Ơ bài 1 nhầm số 4 thành số 2 rồi, bạn sửa lại 1 chút nhé :D
Còn 1 cách làm khác nữa là lượng giác hóa
Đặt \(x^4=2sint\Rightarrow x^3dx=\dfrac{1}{2}cost.dt\)
\(\Rightarrow I=\dfrac{1}{2}\int\dfrac{cost.dt}{\left(4sin^2t-4\right)^2}=\dfrac{1}{32}\int\dfrac{cost.dt}{cos^4t}=\dfrac{1}{32}\int\dfrac{dt}{cos^3t}\)
Đặt \(\left\{{}\begin{matrix}u=\dfrac{1}{cost}\\dv=\dfrac{dt}{cos^2t}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{sint.dt}{cos^2t}\\v=tant\end{matrix}\right.\)
\(\Rightarrow32I=\dfrac{tant}{cost}-\int\dfrac{tant.sint.dt}{cos^2t}=\dfrac{sint}{cos^2t}-\int\dfrac{sin^2t.dt}{cos^3t}\)
\(=\dfrac{sint}{1-sin^2t}-\int\dfrac{1-cos^2t}{cos^3t}dt=\dfrac{sint}{1-sin^2t}-\int\dfrac{dt}{cos^3t}+\int\dfrac{1}{cosx}dx\)
Chú ý rằng \(\int\dfrac{dt}{cos^3t}=32I\)
\(\Rightarrow32I=\dfrac{sint}{1-sin^2t}-32I+\int\dfrac{cost.dt}{cos^2t}\)
\(\Rightarrow64I=\dfrac{sint}{1-sin^2t}-\int\dfrac{d\left(sint\right)}{sin^2t-1}=\dfrac{sint}{1-sin^2t}-\dfrac{1}{2}ln\left|\dfrac{sint-1}{sint+1}\right|+C\)
\(\Rightarrow I=\dfrac{1}{64}\left(\dfrac{2x^4}{4-x^8}-\dfrac{1}{2}ln\left|\dfrac{x^4-2}{x^4+2}\right|\right)+C\)

1/ \(I=\int\limits^1_0\dfrac{2x+1}{x^2+x+1}dx=\int\limits^1_0\dfrac{d\left(x^2+x+1\right)}{x^2+x+1}=ln\left|x^2+x+1\right||^1_0=ln3\)
2/ \(\int\limits^{\dfrac{1}{2}}_0\dfrac{5x}{\left(1-x^2\right)^3}dx=-\dfrac{5}{2}\int\limits^{\dfrac{1}{2}}_0\dfrac{d\left(1-x^2\right)}{\left(1-x^2\right)^3}=\dfrac{5}{4}\dfrac{1}{\left(1-x^2\right)^2}|^{\dfrac{1}{2}}_0=\dfrac{35}{36}\)
3/ \(\int\limits^1_0\dfrac{2x}{\left(x+1\right)^3}dx\Rightarrow\) đặt \(x+1=t\Rightarrow x=t-1\Rightarrow dx=dt;\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=1\Rightarrow t=2\end{matrix}\right.\)
\(I=\int\limits^2_1\dfrac{2\left(t-1\right)dt}{t^3}=\int\limits^2_1\left(\dfrac{2}{t^2}-\dfrac{2}{t^3}\right)dt=\left(\dfrac{-2}{t}+\dfrac{1}{t^2}\right)|^2_1=\dfrac{1}{4}\)
4/ \(\int\limits^1_0\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}dx\)
Kĩ thuật chung là tách và sử dụng hệ số bất định như sau:
\(\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}=\dfrac{ax+b}{x^2+1}+\dfrac{c}{x+2}=\dfrac{\left(a+c\right)x^2+\left(2a+b\right)x+2b+c}{\left(x^2+1\right)\left(x+2\right)}\)
\(\Rightarrow\left\{{}\begin{matrix}a+c=0\\2a+b=4\\2b+c=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=0\\a=-c=2\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^1_0\left(\dfrac{2x}{x^2+1}-\dfrac{2}{x+2}\right)dx=\int\limits^1_0\dfrac{d\left(x^2+1\right)}{x^2+1}-2\int\limits^1_0\dfrac{d\left(x+2\right)}{x+2}=ln\dfrac{8}{9}\)
5/ \(\int\limits^1_0\dfrac{x^2dx}{x^6-9}\Rightarrow\) đặt \(x^3=t\Rightarrow3x^2dx=dt\Rightarrow x^2dx=\dfrac{1}{3}dt;\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(I=\dfrac{1}{3}\int\limits^1_0\dfrac{dt}{t^2-9}=\dfrac{1}{18}\int\limits^1_0\left(\dfrac{1}{t-3}-\dfrac{1}{t+3}\right)dt=\dfrac{1}{18}ln\left|\dfrac{t-3}{t+3}\right||^1_0=-\dfrac{1}{18}ln2\)
6/ Tương tự câu 4, sử dụng hệ số bất định ta tách được:
\(\int\limits^2_1\dfrac{2x-1}{x^2\left(x+1\right)}dx=\int\limits^2_1\left(\dfrac{3x-1}{x^2}-\dfrac{3}{x+1}\right)dx=\int\limits^2_1\left(\dfrac{3}{x}-\dfrac{1}{x^2}-\dfrac{3}{x+1}\right)dx\)
\(=\left(3ln\left|\dfrac{x}{x+1}\right|+\dfrac{1}{x}\right)|^2_1=3ln\dfrac{4}{3}-\dfrac{1}{2}\)

a) =
=
b) =
=
=
c)=
d)=
=
e)=
=
g)Ta có f(x) = sin3xcos5x là hàm số lẻ.
Vì f(-x) = sin(-3x)cos(-5x) = -sin3xcos5x = f(-x) nên:
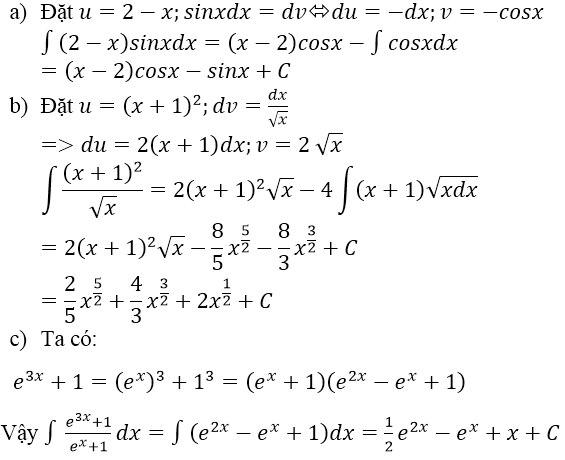

Câu 1:
\(A=\int \frac{2\sin x+\cos x}{3\sin x+2\cos x}dx\)
\(A=\int \frac{\frac{8}{13}(3\sin x+2\cos x)-\frac{1}{13}(3\cos x-2\sin x)}{3\sin x+2\cos x}dx\)
\(A=\frac{8}{13}\int dx-\frac{1}{13}\int \frac{(3\cos x-2\sin x)dx}{3\sin x+2\cos x}\)
\(A=\frac{8}{13}x-\frac{1}{13}\int \frac{d(3\sin x+2\cos x)}{3\sin x+2\cos x}\)
\(A=\frac{8}{13}x-\frac{1}{13}\ln |3\sin x+2\cos x|+c\)
Câu 2:
Ta có: \(I=\int \frac{x^3}{x^4+3x^2+2}dx=\int \frac{x^3}{(x^2+1)(x^2+2)}dx\)
\(=\int x^3\left(\frac{1}{x^2+1}-\frac{1}{x^2+2}\right)dx=\int \frac{x^3dx}{x^2+1}-\int \frac{x^3}{x^2+2}dx\)
\(=\frac{1}{2}\int \frac{x^2d(x^2+1)}{x^2+1}-\frac{1}{2}\int \frac{x^2d(x^2+2)}{x^2+2}\)
\(=\frac{1}{2}\int \left(1-\frac{1}{x^2+1}\right)d(x^2+1)-\frac{1}{2}\int \left(1-\frac{2}{x^2+2}\right)d(x^2+2)\)
\(=\frac{1}{2}\int d(x^2+1)-\frac{1}{2}\int \frac{d(x^2+1)}{x^2+1}-\frac{1}{2}\int d(x^2+2)+\int \frac{d(x^2+2)}{x^2+2}\)
\(=\frac{x^2+1}{2}-\frac{1}{2}\ln |x^2+1|-\frac{x^2+2}{2}+\ln |x^2+2|+c\)
\(=\ln |x^2+2|-\frac{1}{2}\ln |x^2+1|+c\)