Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

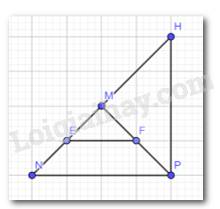
Ta thấy: \(\Delta MEF\)cân tại M do ME = MF có:
+ cạnh bên: ME, MF
+ cạnh đáy: EF
+ góc ở đỉnh: \(\widehat {EMF}\)
+ góc ở đáy: \(\widehat {MEF}\),\(\widehat {MFE}\)
\(\Delta MNP\) cân tại M do MN = MP có:
+ cạnh bên: MN, MP
+ cạnh đáy: NP
+ góc ở đỉnh: \(\widehat {NMP}\)
+ góc ở đáy: \(\widehat {NPM}\), \(\widehat {PNM}\)
\(\Delta MHP\) cân tại M do MH = MP có:
+ cạnh bên : MH, MP
+ cạnh đáy: HP
+ góc ở đỉnh: \(\widehat {PMH}\)
+ góc ở đáy: \(\widehat {MPH}\),\(\widehat {MHP}\)

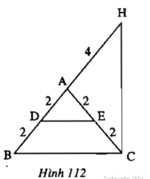
Các tam giác cân trên hình 112:
-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh
-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh
-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh

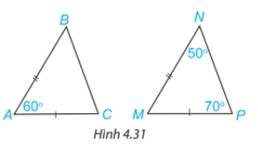
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
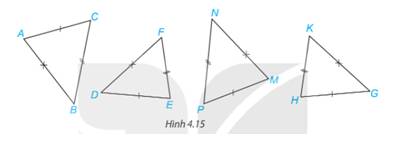
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
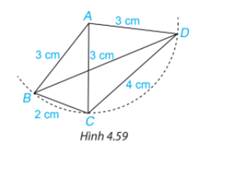





+) Tam giác ABD cân tại đỉnh A có:
AB, AD là 2 cạnh bên
BD là cạnh đáy
\(\widehat B,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ADC cân tại A có:
AC, AD là 2 cạnh bên
DC là cạnh đáy
\(\widehat C,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ABC cân tại A có:
AB, AC là 2 cạnh bên
BC là cạnh đáy
\(\widehat C,\widehat B\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh