CH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Gọi giao điểm của AB và xy là O
\( \Rightarrow \) O là trung điểm AB (Do xy là đường trung trực của AB)
\( \Rightarrow \) Đo khoảng cách AO và từ điểm O kẻ OB sao cho OA = OB và nằm khác phía với điểm A so với đường thẳng xy (A, B, O thẳng hàng)
21 tháng 9 2023
Tham khảo:
a)
- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
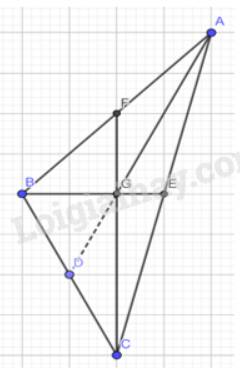
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
\(\dfrac{{BG}}{{BE}} = \dfrac{2}{3};\dfrac{{CG}}{{CF}} = \dfrac{4}{6};\dfrac{{AG}}{{AD}} = \dfrac{{4.4}}{{6.6}}\)
- Ta thấy sau khi rút gọn các tỉ số ta có :
\(\dfrac{{BG}}{{BE}} = \dfrac{{CG}}{{CF}} = \dfrac{{AG}}{{AD}} = \dfrac{2}{3}\)
27 tháng 6 2016
Đầu tiên xác định trung điểm M của AB bằng thước thẳng.
Có AM=BM = \(\frac{AB}{2}=3\left(cm\right)\)
Sau khi xác định được M ta dùng êke vẽ đường thẳng d vuông góc với AB tại M. Từ đó ta có d là đường trung trực của AB.
CM
8 tháng 5 2018
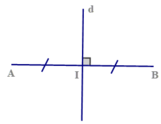
Cách vẽ:
- Vẽ đoạn thẳng AB = 5 cm
- Vẽ trung điểm I của đoạn thẳng AB: Trên tia AB, lấy điểm I sao cho A I = 5 2 = 2 , 5 c m .
- Qua I vẽ đường thẳng d vuông góc với AB. Ta có d là đường trung trực của đoạn thẳng AB
18 tháng 10 2016
A B C a
- Vẽ đoạn thẳng AB và vẽ trung điểm của đoạn thẳng đó ( điểm C )
- Kẻ đường thẳng a đi qua C và vuông góc với AB
=> Ta được đường trung trực của đoạn thẳng ấy
18 tháng 10 2016
B A d Bước 1: Vẽ đoạn thẳng AB dài 28mm. Rồi xác định trung điểm của đoạn thẳng đó sao cho C AC=BC=1/2 AB Bước 2: Vẽ đường thẳng d đi qua điểm c sao cho vuông góc với AB
KN
3 tháng 7 2019
b) Xét \(\Delta AOK\)và \(\Delta BOK\)có:
\(OA=OB\left(gt\right)\)
\(\widehat{AOK}=\widehat{BOK}\)(Vì Oz là phân giác của \(\widehat{xOy}\))
\(OK\): cạnh chung
Suy ra \(\Delta AOK\)\(=\Delta BOK\)(c.g.c)
\(\Rightarrow AK=BK\)(hai cạnh tương ứng)
Mà K nằm giữa A và B nên K là trung điểm của AB (đpcm)
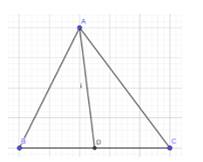
Cách xác định trung điểm của 1 đoạn thẳng:
- Trên 1 đoạn thẳng, điểm đó nằm giữa và cách đều 2 đầu đoạn thẳng đó