Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Ta có: 2x + 3y = 7 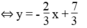
Cho x = 0 thì y = 7/3 ⇒ (0; 7/3 )
Cho y = 0 thì x = 7/2 ⇒ (7/2 ; 0)
*Ta có: x – y = 6 ⇔ y = x – 6
Cho x = 0 thì y = -6 ⇒ (0; -6)
Cho y = 0 thì x = 6 ⇒ (6; 0)
Hai đường thẳng cắt nhau tại M(5; -1) nên nghiệm của hệ phương trình là (x; y) = (5; -1)
Đồ thị:
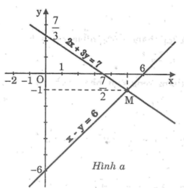

Ta có:
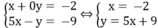
*Vẽ đường thẳng x = -2 song song với trục tung
*Vẽ đường thẳng y = 5x + 9
Cho x = 0 thì y = 9 ⇒ (0; 9)
Cho y = 0 thì x = - 9/5 = -1,8
Hai đường thẳng y = 5x + 9 và x = -2 cắt nhau tại A(-2; -1). Vậy hệ phương trình có một nghiệm duy nhất (x; y) = (-2; -1).
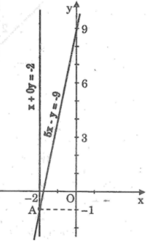

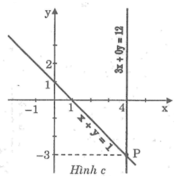
*Ta có: x + y = 1 ⇔ y = -x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1 ⇒ (1; 0)
*Ta có: 3x + 0y = 12 ⇔ x = 4
Hai đường thẳng cắt nhau tại P(4; -3) nên nghiệm của hệ phương trình là (x; y) = (4; -3)
Đồ thị:

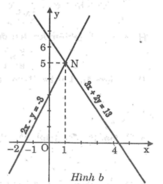
*Ta có: 3x + 2y = 13 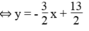
Cho x = 0 thì y = 13/2 ⇒ (0; 13/2 )
Cho y = 0 thì x = 13/3 ⇒ (13/3 ; 0)
*Ta có: 2x – y = -3 ⇔ y = 2x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = - 3/2 ⇒ (- 3/2 ; 0)
Hai đường thẳng cắt nhau tại N(1; 5) nên nghiệm của hệ phương trình là (x; y) = (1; 5).
Đồ thị:

Xét (II): 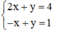
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
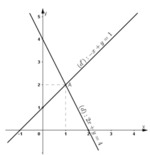
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
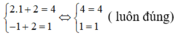
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).

a) Xét hệ (I): 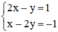
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.
+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1
Chọn x = 0 ⇒ y = -1.
Chọn y = 0 ⇒ x = 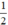
⇒ (d) đi qua hai điểm (0; -1) và 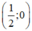
+ Xét (d’) : x – 2y = -1 hay (d’): 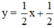
Chọn x = 0 ⇒ y = 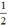
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm 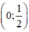 và (-1; 0).
và (-1; 0).
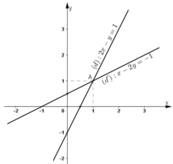
Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).
Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:
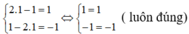
Vậy hệ phương trình (I) có một nghiệm là (1; 1)
b) Xét (II): 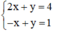
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
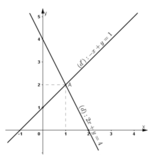
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
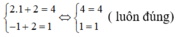
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).

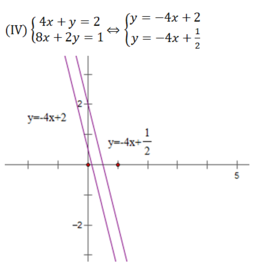
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
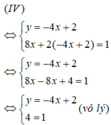
Vậy hệ phương trình (IV) vô nghiệm.

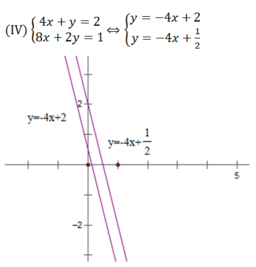
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
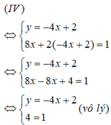
Vậy hệ phương trình (IV) vô nghiệm.

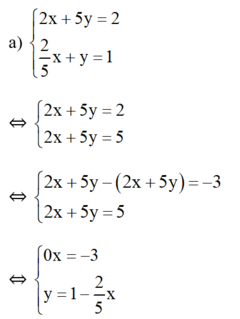
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
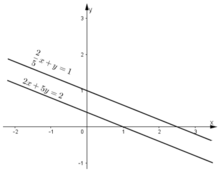
Minh họa hình học:
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng 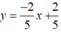 (d1)
(d1)
Tập nghiệm của phương trình 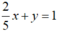 được biểu diễn bởi đường thẳng
được biểu diễn bởi đường thẳng 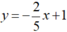 (d2).
(d2).


KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm
(1): x+y=4
=>y=4-x
(2): 2x-y=-1
=>y=2x+1