Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình của bài như thế này phải không ? Nếu như thế thì mk giải cho ! Bài này cô mk dạy rồi !
Phân tích : Vì BP = \(\frac{1}{3}\)BC và hai hình tam giác : ABP và ABC có chung chiều cao hạ từ đỉnh A xuống đáy BC nên diện tích tam giác ABP bằng \(\frac{1}{3}\)diện tích tam giác ABC.
Tượng tự,diện tích mỗi hình tam giác BCM và CAN cũng bằng \(\frac{1}{3}\)diện tích tam giác ABC.
Vậy tổng diện tích ba tam giác : ABP , BMC , CAN bằng diện tích tam giác ABC.
Về mặt lý thuyết thì chúng có thể phủ kín tam giác ABC . Nhưng thật ra chúng để thừa lại phần diện tích tam giác IEF và chũng lại phủ lên các tam giác: IMC , EAN , FBP mỗi tam giác phủ hai lần nên thừ ra một lần . Chính điều này chứng tỏ :
SFBP + SEAN + SIMC = SIEF
Chúc bạn hok tốt !
A B C M N E I F

Giải thích các bước giải:
Bài làm
Trong ΔABC, ta có: D là trung điểm BC
ED = 1/2 AE
⇒E là trọng tâm của ΔABC
Mà BE cắt AC tại G
⇒G cũng là trung điểm của AC.
Giải thích các bước giải:
Bài làm
Trong ΔABC, ta có: D là trung điểm BC
ED = 1/2 AE
⇒E là trọng tâm của ΔABC
Mà BE cắt AC tại G
⇒G cũng là trung điểm của AC.

A B C D M N
Ta có: \(S_{AMN}=\frac{BN.AM}{2}=\frac{BN\cdot\frac{1}{2}AB}{2}\)
\(S_{ABN}=\frac{AB.BN}{2}\)
=> \(\frac{S_{AMN}}{S_{ABN}}=\frac{\frac{\frac{1}{2}BN.AB}{2}}{\frac{AB.BN}{2}}=\frac{1}{2}\) => \(S_{AMN}=\frac{1}{2}S_{ABN}\)(1)
Ta lại có: BN = 2NC; BN + NC = BC => BN = 2/3BC
\(S_{ABN}=\frac{AB.BN}{2}=\frac{AB\cdot\frac{2}{3}BC}{2}\)
\(S_{ABCD}=AB.BC\)
\(\frac{S_{ABN}}{S_{ABCD}}=\frac{\frac{\frac{2}{3}AB.BC}{2}}{AB.BC}=\frac{1}{3}\) => \(S_{ABN}=\frac{1}{3}S_{ABCD}\) => \(\frac{1}{2}S_{ABN}=\frac{1}{6}S_{ABCD}\)(2)
Từ (1) và (2) => \(S_{AMN}=\frac{1}{6}S_{ABCD}\)
awbb ưieaaaaaaaa
r
ewfrsd
tf
sdfdyufee
e
ẻ
r
re
ê
r
e
ẻ
e
re
ẻ
rr

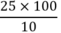 =2500
(
m
2
)
=2500
(
m
2
)
Chịu! Có hình đâu?
dung co hinh dau