KS
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
3
10 tháng 10 2021
\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)
Khi \(M=\sqrt{x}-2\)
\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)
\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)
Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)
AP
21 tháng 10 2018
\(\sqrt{81.16.169}=\sqrt{81}.\sqrt{16}.\sqrt{169}=9.4.13=468\)
\(\sqrt{10}.\sqrt{810}=\sqrt{10.10}.\sqrt{81}=10.9=90\)
\(\sqrt{64}.\sqrt{81.100}-\sqrt{64}.\sqrt{196.16}=\sqrt{64}\left(\sqrt{81}.\sqrt{100}-\sqrt{196}.\sqrt{16}\right)=8.\left(9.10-14.4\right)=8.34=272\)
12 tháng 2 2020
Đặt \(A=\sqrt{x^2-6x+36}+\sqrt{x^2-6x+64}=18\)
\(B=\sqrt{x^2-6x+64}-\sqrt{x^2-6x+36}\)
\(\Rightarrow A.B=\left(x^2-6x+64\right)-\left(x^2-6x+36\right)=28\)
mà \(A=18\Rightarrow B=\frac{28}{18}=\frac{14}{9}\)
20 tháng 7 2016
Ta có : \(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\frac{x+y+z}{2}\Leftrightarrow2\sqrt{x}+2\sqrt{y-1}+2\sqrt{z-2}=x+y+z\)
\(\Leftrightarrow\left(x-2\sqrt{x}+1\right)+\left(y-1-2\sqrt{y-1}+1\right)+\left(z-2-2\sqrt{z-2}+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\)
Vì \(\left(\sqrt{x}-1\right)^2\ge0\) , \(\left(\sqrt{y-1}-1\right)^2\ge0\), \(\left(\sqrt{z-2}-1\right)^2\ge0\) nên phương trình trên tương đương với
\(\hept{\begin{cases}\left(\sqrt{x}-1\right)^2=0\\\left(\sqrt{y-1}-1\right)^2=0\\\left(\sqrt{z-2}-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}}\)
Từ đó tính được : \(x^2+y^2+z^2=1^2+2^2+3^2=14\)
20 tháng 7 2016
Ta có:
\(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}\)
=\(\sqrt{x.1}+\sqrt{\left(y-1\right).1}+\sqrt{\left(z-2\right).1}\)
\(\le\frac{x+1}{2}+\frac{y-1+1}{2}+\frac{z-2+1}{2}\)
=\(\frac{x+y+z}{2}\)
Dấu"=" xảy ra khi \(\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}\)
Ta có:x2+y2+z2=1+22+32=14
AH
Akai Haruma
Giáo viên
3 tháng 10 2018
Câu 1:
ĐK: \(x\geq \frac{-3}{2}\)
\(\sqrt{2x+3}=3-\sqrt{5}\)
\(\Rightarrow 2x+3=(3-\sqrt{5})^2=14-6\sqrt{5}\)
\(\Rightarrow x=\frac{11-6\sqrt{5}}{2}\)
Câu 2: ĐK: \(x\geq 0\)
\(\sqrt{5+\sqrt{7x}}=2+\sqrt{7}\)
\(\Rightarrow 5+\sqrt{7x}=(2+\sqrt{7})^2=11+4\sqrt{7}\)
\(\Rightarrow \sqrt{7x}=6+4\sqrt{7}\)
\(\Rightarrow 7x=(6+4\sqrt{7})^2\Rightarrow x=\frac{(6+4\sqrt{7})^2}{7}\)
AH
Akai Haruma
Giáo viên
3 tháng 10 2018
Câu 3: ĐK: \(x\geq 0\)
\((\sqrt{x}-2)(5-\sqrt{x})=4-x\)
\(\Leftrightarrow 5\sqrt{x}-x-10+2\sqrt{x}=4-x\)
\(\Leftrightarrow 7\sqrt{x}=14\Rightarrow \sqrt{x}=2\Rightarrow x=4\)
Câu 4: ĐK: \(x\ge 1\)
Sửa đề \(\frac{1}{2}\sqrt{x-1}-\frac{3}{2}\sqrt{9x-9}+24\sqrt{\frac{x-1}{64}}=-17\)
\(\Leftrightarrow \frac{\sqrt{x-1}}{2}-\frac{3}{2}\sqrt{9}.\sqrt{x-1}+24\sqrt{\frac{1}{64}}\sqrt{x-1}=-17\)
\(\Leftrightarrow \frac{\sqrt{x-1}}{2}-\frac{9\sqrt{x-1}}{2}+3\sqrt{x-1}=-17\)
\(\Leftrightarrow \sqrt{x-1}(\frac{1}{2}-\frac{9}{2}+3)=-17\)
\(\Leftrightarrow -\sqrt{x-1}=-17\Rightarrow \sqrt{x-1}=17\Rightarrow x=17^2+1=290\)
NC
27 tháng 8 2020
Cái đầu là tính à?
Ta có: \(\left(\sqrt{15}+2\sqrt{3}\right)^2+12\sqrt{5}\)
\(=\left(\sqrt{15}\right)^2+2.2\sqrt{3}.\sqrt{15}+\left(2\sqrt{3}\right)^2+12\sqrt{5}\)
\(=15+12\sqrt{5}+12+12\sqrt{5}\)
\(=27+24\sqrt{5}\)
Sau:
Ta thấy: Điều kiện để \(\sqrt{-\left|x+5\right|}\) có nghĩa là \(-\left|x+5\right|\ge0\left(\forall x\right)\)
Mà \(-\left|x+5\right|\le0\left(\forall x\right)\) nên dấu "=" xảy ra khi: \(\left|x+5\right|=0\Rightarrow x=-5\)
Vậy khi x = -5 thì \(\sqrt{-\left|x+5\right|}\) có nghĩa
27 tháng 8 2020
Làm lại ý 2
\(\sqrt{-\left|x+5\right|}\)có nghĩa
\(\Leftrightarrow-\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|\le0\)
\(\Leftrightarrow x+5\le0\)
\(\Leftrightarrow x\le-5\)
VT
30 tháng 9 2019
đặt \(\sqrt{x^2-6x+36}=\)M;\(\sqrt{x^2-6x+64}=\)N ,hiển nhiên M\(\ne\)N
M+N=7 <=>(M+N)(M-N)=7(M-N) <=>M2-N2=7(M-N) <=>-28=7(M-N) <=>N-M=4
A=2N-2M=2.4=8
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 8 2021
Đặt \(\sqrt{x^2-6x+36}=a\ge0\Rightarrow\sqrt{x^2-6x+64}=\sqrt{a^2+28}\)
Vậy ta có phương trình :
\(a+\sqrt{a^2+28}=7\Leftrightarrow\sqrt{a^2+28}=7-a\Leftrightarrow\hept{\begin{cases}a\le7\\a^2+28=a^2-14a+49\end{cases}\Leftrightarrow a=\frac{3}{2}}\)
ta có : \(A=\sqrt{4\left(x^2-6x+36\right)+112}-2\sqrt{x^2-6x+36}=\sqrt{4a^2+112}-2a=8\)
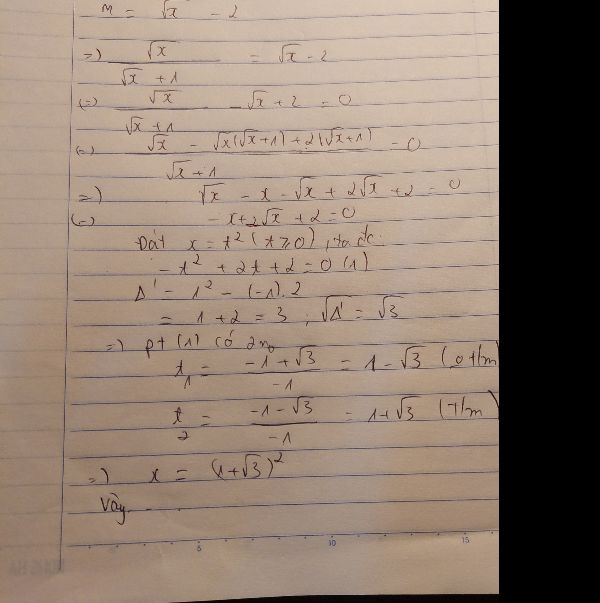
bằng 8
nhanh nha mn