Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toàn bộ năng lượng đến trong 1s là:
\(E_1=N_1\frac{hc}{\lambda_1}\)
Năng lượng hạt phát ra trong 1s là :
\(E_2=N_2\frac{hc}{\lambda_2}\)
mặt khác ta có
\(E_2=H.E_1\)
\(N_2\frac{hc}{\lambda_2}=HN_1\frac{hc}{\lambda_1}\)
\(\frac{N_2}{\lambda_2}=H\frac{N_1}{\lambda_1}\)
\(N_2=H\frac{N_1\lambda_2}{\lambda_1}=2.4144.10^{13}hạt\)

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

độ phóng xạ \(\beta^-\) của một tượng gỗ bằng 0,8 lần độ phóng xạ của một khúc gỗ cùng khối lượng lúc mới chặt

1Bình chọn giảm
Trong trường hợp ban đầu giotj thủy ngân nằm chính giữa nên thể tích 2 phần bằng nhau
Tỉ số này không đổi do khí vẫn được giữ cố định trong bình.
Khi cùng tăng nhiệt độ của 2 bình lên 1 lượng nhỏ thì tỉ số giua 2 nhiệt độ thay đổi dẫn đến tỉ lệ thể tích thay đổi. Bên nào thể tích nhỏ hơn thì là do giotj thủy ngân dịch về phía đó.
Tỷ số giua 2 nhiệt độ phụ thuộc (T1 > T2 hay không)
Nêú biết bên nào có nhiệt độ cao hơn sẽ biết thủy ngân dịch về bên nào

Bạn tham khảo hai bài tương tự này nhé:
Câu hỏi của Nguyễn Khánh Quỳnh - Học và thi online với HOC24
Câu hỏi của Hue Le - Học và thi online với HOC24

1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)
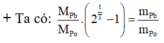
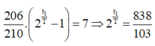
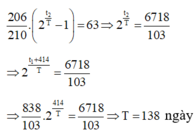

Đáp án B