Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(f\left(x\right)=y=\frac{x^2+mx}{1-x}\Rightarrow y'=\frac{\left(2x+mx\right)\left(1-x\right)+\left(x^2+mx\right)}{\left(1-x\right)^2}=\frac{-x^2+2x+m}{\left(1-x\right)^2}\)\(\)\(\left(D=R/\left\{1\right\}\right)\)
Đặt \(g\left(x\right)=-x^2+2x+m\)\(\Rightarrow\)f(x) cùng dấu với y' trên D
Xét pt g(x)=0
\(\Delta'=m+1\), Hàm số có 2 điểm cực trì<=> pt có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ne0\end{cases}\Leftrightarrow m>-1}\)
Khi đó 2 điểm cực trì là A(x1,f(x1) ) và B(x2, f(x2) )
Lại có \(f'\left(x_1\right)=\frac{\left(2x_1+m\right)\left(1-x_1\right)+\left(x_1^2+mx_1\right)}{\left(1-x_1\right)^2}=0\Rightarrow x_1^2+mx_1=-\left(2x_1+m\right)\left(1-x_1\right)\)
\(\Rightarrow f\left(x_1\right)=\frac{x_1^2+mx_1}{1-x_1}=-2x_1-m.\)
=>\(f\left(x_2\right)=-2x_2-m\)
Khoảng cách giữa 2 điểm cực trị:
\(AB=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{\left(x_1-x_2\right)^2+\left(2x_1-2x_2\right)^2}=|x_1-x_2|\sqrt{5}=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=20\)
A/d Vi-ét cho pt g(x)=0\(\Rightarrow4+4m=20\Leftrightarrow m=4\)
Vậy m=4

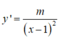
Để hàm số tăng trên từng khoảng xác định thì y’ > 0 <=> m > 0.
Chọn A

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

Tập xác định :
Nếu hàm số đạt cực đại tại x = 2 thì y'(2) = 0 ⇔ m2 + 4m + 3 = 0 ⇔ m=-1 hoặc m=-3
- Với m = -1, ta có :
x=0 hoặc x=2.
Ta có bảng biến thiên :
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
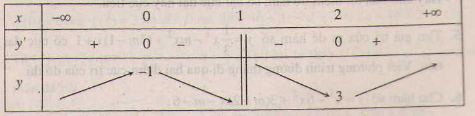
- Với m = -3, ta có:
x=2 hoặc x=4
Ta có bản biến thiên :
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.

Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng (− ∞ ; m), (m; + ∞ ) khi và chỉ khi:
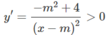
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2


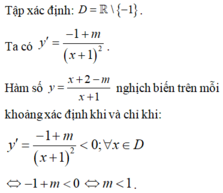
\(y=\dfrac{-x^2+mx-2}{x+1}\)
\(y'=\dfrac{\left(-2x+m\right)\left(x+1\right)-\left(-x^2+mx-2\right)}{\left(x+1\right)^2}=\dfrac{-x^2-2x+m+2}{\left(x+1\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi:
\(-x^2-2x+m+2\le0;\forall m\)
\(\Leftrightarrow\Delta'=1+\left(m+2\right)\le0\)
\(\Rightarrow m\le-3\)