
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hàm số
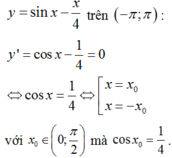
Bảng biến thiên:
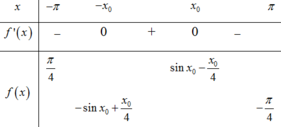
Do y = sin x - x 4 là hàm lẻ nên đồ thị hàm số y = sin x - x 4 nhận O(0;0) là tâm đối xứng.
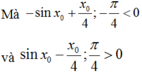
Đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt x 1 ; x 2 ; x 3 ( x 1 ; x 2 ; x 3 khác ± x 0 )
Số điểm cực trị của hàm số số y = sin x - π 4 ; x ∈ - π ; π là: 2 + 2 = 4
Chọn B.

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

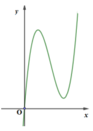

Để đồ thị hàm số có 2 điểm cực trị thì
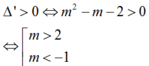
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
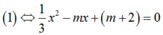
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
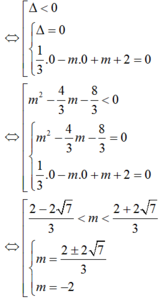
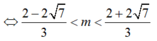
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A
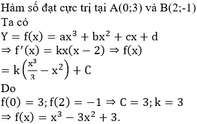
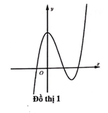
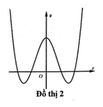
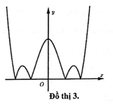
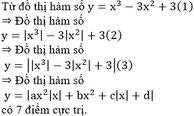
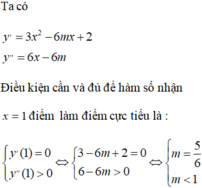
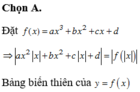
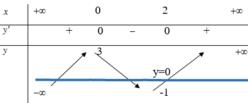
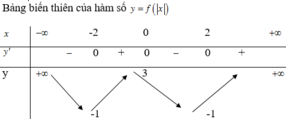
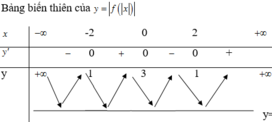
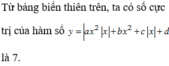


Đáp án C
Ta có y ' = 1 - 2 cos 2 x ⇒ y ' = 0 ⇔ cos 2 x = 1 2 ⇒ x = ± π 6 + k π hơn nữa y ' đổi dấu từ dương sang âm qua điểm - π 6 nên x = - π 6 là điểm cực tiểu của hàm số. (Ta có thể tính y ' ' = 4 s in 2 x ⇒ y ' ' ( π 6 ) < 0 ⇒ - π 6 là điểm cực đại của hàm số)