NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 5 2017
a) Đồ thị của hàm số \(y=\log_3\left(x-1\right)\) nhận được từ đồ thị của hàm số \(y=\log_3x\) bằng cách tịnh tiến song song với trục hoành sang bên phải 1 đơn vị
b) Đồ thị của hàm số \(y=\log_{\dfrac{1}{3}}\left(x+1\right)\) nhận được từ đồ thị của hàm số \(y=\log_{\dfrac{1}{3}}x\) bằng cách tịnh tiến song song với trục hoành sang bên trái 1 đơn vị
c) Đồ thị của hàm số \(y=1+\log_3x\) nhận được từ đồ thị của hàm số \(y=\log_3x\) bằng cách tịnh tiến song song với trục tung lên trên 1 đơn vị
G
14 tháng 5 2016
a. \(y=\left(3^x-9\right)^{-2}\)
Điều kiện : \(3^x-9\ne0\Leftrightarrow3^x\ne3^2\)
\(\Leftrightarrow x\ne2\)
Vậy tập xác định là \(D=R\backslash\left\{2\right\}\)
b. \(y=\sqrt{\log_{\frac{1}{3}}\left(x-3\right)-1}\)
Điều kiện : \(\log_{\frac{1}{3}}\left(x-3\right)-1\ge0\Leftrightarrow\log_{\frac{1}{3}}\left(x-3\right)\ge1=\log_{\frac{1}{3}}\frac{1}{3}\)
\(\Leftrightarrow0< x-3\le\frac{1}{3}\)
\(\Leftrightarrow3< x\le\frac{10}{3}\)
Vậy tập xác định \(D=\) (3;\(\frac{10}{3}\)]
c. \(y=\sqrt{\log_3\sqrt{x^2-3x+2}+4-x}\)
Điều kiện :
\(\log_3\sqrt{x^2-3x+2}+4-x\ge0\Leftrightarrow x^2-3x+2+4-x\ge1\)
\(\Leftrightarrow\sqrt{x^2-3x+2}\ge-x-3\)
\(\Leftrightarrow\begin{cases}x-3< 0\\x^2-3x+2\ge0\end{cases}\) hoặc \(\begin{cases}x-3\ge0\\x^2-3x+2\ge\left(x-3\right)^2\end{cases}\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x\le1\\2\le x< 3\\x\ge3\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x\le1\\x\ge2\end{array}\right.\)
Vậy tập xác định là : D=(\(-\infty;1\)]\(\cup\) [2;\(+\infty\) )
PT
Tìm m để hàm số sau xác định với mọi \(x\in R\) :
\(y=\frac{1}{\sqrt{\log_3\left(x^2-2x+3m\right)}}\)
1
6 tháng 5 2016
Hàm số xác định với mọi \(x\in R\) khi và chỉ khi
\(\log_3\left(x^2-2x+3m\right)>0,x\in R\)
\(x^2-2x+3m>1,x\in R\Leftrightarrow x^2-2x+3m-1>0x\in R\)
Vì \(a=1>0\) nên \(\Delta'< 0\Leftrightarrow1-\left(3m-1\right)< 0\Leftrightarrow m>\frac{2}{3}\)
Vậy với \(m>\frac{2}{3}\) thì hàm số đã cho xác định với mọi \(x\in R\)
GV
Giáo viên Toán
Giáo viên
4 tháng 5 2017
Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).
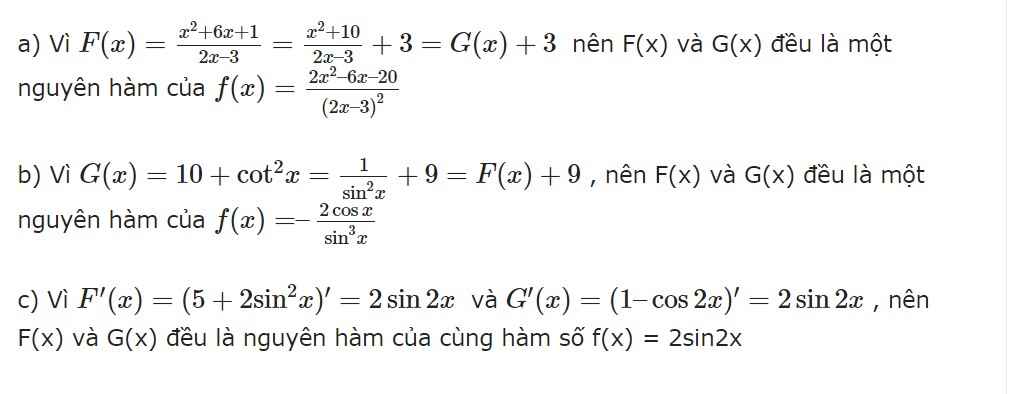
\(f'\left(x\right)=\frac{\left(\sin x\right)'}{\sin x.\ln3}=\frac{\cos x}{\sin x.ln3}=\frac{\cot x}{ln3}\)