Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
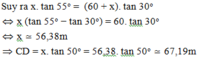
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C

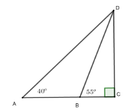
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A

Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m

- Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B
\(\Rightarrow tan60=\dfrac{h}{BC}\)
\(\Rightarrow BC=\dfrac{h\sqrt{3}}{3}\)
\(\Rightarrow BD=BC+CD=\dfrac{h\sqrt{3}}{3}+600\)
- Áp dụng tỉ số lượng giác vào tam giác ABD vuông tại B
\(tan50=\dfrac{h}{BD}\)
\(\Rightarrow h=tan50.\left(\dfrac{h\sqrt{3}}{3}+600\right)\)
\(\Rightarrow h\approx2292m\)
Vậy ...

Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
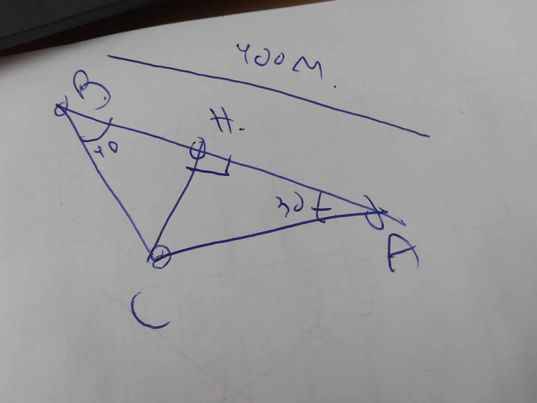
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)

2. Để MONP là hình vuông thì đường chéo OM=ON\(\sqrt{2}\)=R\(\sqrt{2}\)
Dựng điểm M: Ta dựng hình vuông OACD, dựng đường tròn tâm O đi qua điểm D, cắt (d) tại M
CM: Từ M vã 2 tiếp tuyến MN và MP ta có: \(MN=\sqrt{MO^2-ON^2}=R\)
Nên tam giác ONM vuông cân tại N. Tương tự tam giác OMP vuông cân tại P do đó MNOP là hình vuông
Bài toán luôn có 2 nghiệm vì \(OM=R\sqrt{2}>R\)
3. Ta có MN và MP là 2 tiếp tuyến của (O) nên MNOP là tứ giác nội tiếp đường tròn đường kính OM. Tâm là trung điểm H của OM. Suy ra tam giác cân MPO nội tiếp trong đường tròn đường kính OM, tâm là H
Kẻ \(OE\perp AB\) thì E là trung điểm của AB (cố định ). kẻ \(HL\perp\left(d\right)\) thì HL//OE nên HL là đường trung bình của tam giác OEM => HL=1/2 OE (không đổi)
Do đó khi M di động trên (d) thì H luôn cách đều (d) một đoạn không đổi, nên H chạy trên đường thẳng (d')//(d) và (d') đi qua trung điểm của đoạn OE
Ta có OM là phân giác góc NMP (tính chất 2 tiếp tuyến cắt nhau). Kẻ tia phân giác góc PNM cắt đường tròn (O) tại điểm F khi đó NF=FP (ứng với góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung bằng nhau)
=> F ở trên OM dó đó F là tâm đường tròn nội tiếp tam giác MNP
Vậy khi M di động trên (d) thì tâm đường tròn nội tiếp tam giác MNP chạy trên đường tròn (O)
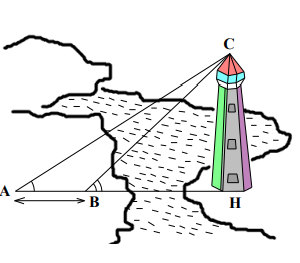 Hình
Hình