Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Giả sử MNPQ là hình chữ nhật
=> ^QMN=90do HAY QM vuong goc voi MN
Lai co MN//BC
=> BC vuong goc voi QM
Ma QM //AO
=> AO vuong goc voi BC
=> O thuoc duong cao ke tu A den BC
Goi giao diem cua AO VA BC LA H
Để SMNPQ=SABC
=> MQ.QP=(BC.AH)/2
Mà QP=BC/2
=> MQ=AH
Ma MQ=AH/2
=> AH=AO/2
Mà AO hay AH vuong goc voi BC
=> BC la trung truc cua AO .
Vay de tu giac MNPQ vua la HCN vua co dien h =tam giac ABC thi BC phai la trung truc cua AO
a,Do tia AO nằm giữa tia AB và tia AC(gt)
Gọi O là điểm nằm giữa đoạn thẳng BC
sao cho BO< OC
M,N,P,Q lần lượt là trung điểm của OB,OC,AC,AB (gt)
=>BM=MO;ON=NC;CP=PA;AQ=QB
Vậy ta có:PQ là đường trung bình của tam giác ABC nên PQ//=1/2 BC (1)
Tương tự:
PN là đường trung bình của tam giác ACO nên PN//=1/2 AO (2)
QM là đường trung bình của tam giác ABO nên QM//=1/2 AO (3)
Từ (2),(3) suy ra:
PN//=QM=1/2 OA ( t/c 2 đường thẳng//) (4)
Do đó PQ//=MN
=> Tứ giác MNPQ là hình bình hành
b,theo cmt : PN//=QM=1/2 OA
Mặt khác, AO là cạnh đối diện của 2 góc B và góc C
Từ đó=>góc B=góc C
=> tam giác ABC cân tại A
=>O là trung điểm của BC
=>AO _|_BC nên góc AOB=góc AOC=90°
=> 3 điểm B,O,C thẳng hàng (vì BOC=180°=góc AOB+góc AOC)
M,N là trung điểm của OB và OC(gt)
nên B,M,O,N,C thẳng hàng.
=>QM_|_BC và PN_|_BC
Hay góc QMN=góc PNM=1 vuông (5)
Theo (1) PQ//BC
=>PQ_|_QM ; PQ_|_PN
Hay góc MQP=góc NPQ=1 vuông (6)
Từ (5),(6) suy ra:
Tứ giác MNPQ là hình chữ nhật (đpcm)

c) Giả thuyết: tứ giác ANMP là hình chữ nhật thì hình bình hành ANMP vuông tại A
=> \(\Delta ABC\)vuông tại A
Vậy: DK để tứ giác ANMP là hình chữ nhật thì \(\Delta ABC\)phải vuông tại A
d) Để tứ giác ANMP là hình vuông thì:
+ Tứ giác ANMP phải là hình thoi
+ Tứ giác ANMP có 1 góc vuông
(Dựa vào DHNB thứ 4: Hình thoi có một góc vuông là hình vuông)
Do đó: Để tứ giác ANMP là hình vuông thì: M phải là giao điểm của phân giác góc A và cạnh BC; đồng thời tứ giác ANMP có một góc vuông tại A(kết hợp kết quả câu b và c)
Hok tốt ~
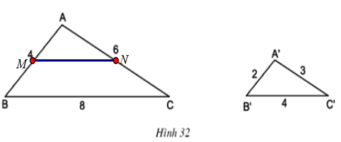


⇒ MN // BC (định lí Ta lét đảo)
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).