Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Bước sóng của sóng λ = 2 π v ω = 2 π . 40 20 π = 4 cm.
Xét tỉ số A N - B N λ = 10 4 = 2 , 5 → N nằm trên điểm đứng yên thứ 3 về phía B.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

\(\lambda =\frac{v}{f}=\frac{50}{10}=5cm.\)
Điểm M ngược pha với điểm I khi: \(\triangle \phi=\phi_I-\phi_M = 2\pi \frac{d_1-d_{1}^{'}}{\lambda}=(2k+1)\pi \Rightarrow d_1-d_1^{'}=(2k+1)\frac{\lambda}{2}\)
Để điểm M gần I nhất thì hiệu d1 - d1' cũng phải nhỏ nhất khi đó k chỉ nhận giá trị nhỏ nhất là k = 0.
\(d_{1}-d_{1}^{'}=(2.0+1)\frac{5}{2}=2.5cm\Rightarrow d_1 = 7.5cm.\)
\(\Rightarrow MI= \sqrt {d_1^{2}-d_1^{'2}}\) = \(\sqrt{7.5^2-2.5^2}=\sqrt{50}cm\)

Tại P dao động cực tiểu khi \(d_{2}-d_{1}=(2k+1+\frac{\triangle \phi}{\pi})\frac{\lambda}{2}.\)
Tại P dao động cực đại khi \(d_{2}-d_{1}=(k+\frac{\triangle \phi}{2\pi})\lambda.\)
Tại M là vân lồi bậc k và tại N là vân lồi bậc k + 3 =>\(MA-MB=(k+0.5)\lambda=12.25\\ NA-NB=(k+3+0.5)\lambda=33.25\\ \)
\(\Rightarrow 3\lambda=33.25-12.25=21 \Rightarrow \lambda=7mm.\)
Số điểm cực đại giao thoa trên đoạn AB là \(-AB\leq (k+\frac{1}{2})\lambda\leq AB \Rightarrow \frac{-AB}{\lambda}-0.5 \leq k \leq \frac{AB}{\lambda}\)
=> có 14 điểm cực đại giao thoa kể cả A và B.
Đáp án D
+ Bước sóng của sóng
Xét tỉ số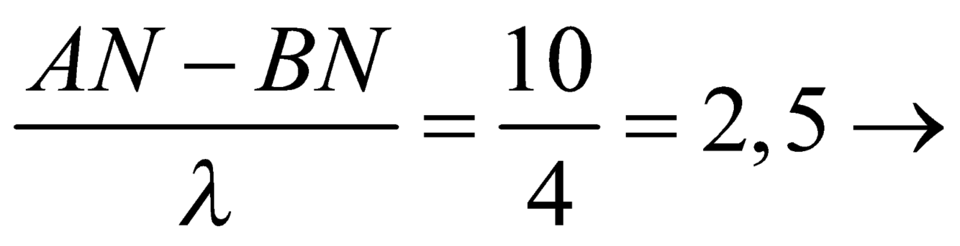
N nằm trên điểm đứng yên thứ 3 về phía B