
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

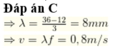

Đáp án B
+ Giả sử rằng cả M và N là các cực đại giao thoa (hoặc cực tiểu không ảnh hưởng đến kết quả bài toán). Khi đó ta có:
MA - MB = kλ = 100 NA - NB = ( k + 5 ) λ = 30 ⇒ 5 λ = 20 ⇒ λ = 4 mm .
+ Từ phương trình sóng, ta có ω = 100 π rad / s ⇒ T = 0 , 02 s .
=> Vận tốc truyền sóng v = λ/T = 4/0,02 = 200 mm/s = 20 cm/s.

Tại P dao động cực đại khi \(d_{2}-d_{1}=(k+\frac{\triangle \phi}{2\pi})\lambda.\)
Tại M là vân lồi bậc k và tại N là vân lồi bậc k + 3 =>\(MA-MB=(k+0.5)\lambda=12.25\\ NA-NB=(k+3+0.5)\lambda=33.25\\ \)
\(\Rightarrow 3\lambda=33.25-12.25=21 \Rightarrow \lambda=7mm.\)
Số điểm cực đại giao thoa trên đoạn AB là \(-AB\leq (k+\frac{1}{2})\lambda\leq AB \Rightarrow \frac{-AB}{\lambda}-0.5 \leq k \leq \frac{AB}{\lambda}\)
=> có 14 điểm cực đại giao thoa kể cả A và B.

\(\Delta \varphi = -\frac{\pi}{2}\)
Người ta thấy vân lồi bậc k đi qua điểm M tức là M thuộc dãy cực đại thứ k: \(MA -MB = (k+ \frac{\Delta \varphi}{2\pi}) \lambda = (k-\frac{1}{4}) \lambda = 12,25mm.(1)\)
Tương tự, N thuộc dãy cực đại thứ k+3 tức là \(NA -NB = (k+3-\frac{1}{4}) \lambda = 33,25mm.(2)\)
Chia (2) cho (1) ta được: \(\frac{k+3-0,25}{k-0,25} = \frac{33.25}{12.25} \)
=> \(k = 2\)
thay vào (1) => \(\lambda = 7m m.\)
Số điểm cực đại trên đoạn AB thỏa mãn: \(-AB < (k - \frac{1}{4}) \lambda < AB\)
=> \(50 < (k-0.25).7 < 50\)
=> \(-6.89< k < 7.39\)
=> \(k = -6,-5,...0,..7\) Số giá trị của k thỏa mãn là:số đầu - số cuối +1 = \(7-(-6)+1 = 14.\)

Đáp án B
+ M và N cùng loại do vậy ta luôn có hiệu số:
∆ d N - ∆ d M = 2 λ ⇒ λ = 3 cm.
+Xét tỉ số S 1 P - S 2 P λ = - 6 , 9 có 13 điểm cực đại trên PQ


\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

\(\lambda =\frac{v}{f}=\frac{50}{10}=5cm.\)
Điểm M ngược pha với điểm I khi: \(\triangle \phi=\phi_I-\phi_M = 2\pi \frac{d_1-d_{1}^{'}}{\lambda}=(2k+1)\pi \Rightarrow d_1-d_1^{'}=(2k+1)\frac{\lambda}{2}\)
Để điểm M gần I nhất thì hiệu d1 - d1' cũng phải nhỏ nhất khi đó k chỉ nhận giá trị nhỏ nhất là k = 0.
\(d_{1}-d_{1}^{'}=(2.0+1)\frac{5}{2}=2.5cm\Rightarrow d_1 = 7.5cm.\)
\(\Rightarrow MI= \sqrt {d_1^{2}-d_1^{'2}}\) = \(\sqrt{7.5^2-2.5^2}=\sqrt{50}cm\)

Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Hai khe được chiếu bằng bức xạ có bước sóng 0,6 μmμm. Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm một khoảng 5,4 mm có
A. vân sáng bậc 2
B. vân sáng bậc 4
C. vân sáng bậc 3
D. vân sáng thứ 4