Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ. Theo giả thiết P(X)=1/5
Gọi Y là biến cố: “người thứ hai ném trúng rổ.Theo giả thiết P(Y)=2/7
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
![]()
Chọn D.

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ.“=> P x = 1 5
Gọi Y là biến cố: “người thứ hai ném trúng rổ.“=> P Y = 2 7
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P(A)=P(X.Y)=P(X).P(Y)= 1 5 . 2 7 = 2 35
Chọn đáp án D

Phép thử T được xét là: "Hai xạ thủ cùng bắn vào bia".
Theo đề ra ta có = "Người thứ k không bắn trúng", k = 1, 2. Từ đó ta có:
a) A = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai không bắn trúng". Suy ra A = .
.
Tương tự, ta có B = "Cả hai đều bắn trúng" = .
.
Xét C = "Có đúng một người bắn trúng", ta có C là hợp của hai biến cố sau:
"Người thứ nhất bắn trúng và người thứ hai bắn trượt" = A1 . .
"Người thứ nhất bắn trượt và người thứ hai bắn trúng" = . A2 .
Suy ra C = A1 . ∪
. A2 .
Tương tự, ta có D = A1 ∪ A2 .
b) Gọi là biến cố: " Cả hai người đều bắn trượt". Ta có
=
.
= A.
Hiển nhiên B ∩ C = Φ nên suy ra B và C xung khắc với nhau.

Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia” i = 1,2.
Khi đó, P(A1) =1/2; P(A2) = 1/3; A1 và A2 độc lập với nhau
X =A1∩ A2 nên P(X) = P(A1∩ A2) = P(A1.A2) = P(A1).P(A2) = 1/6
Chọn đáp án là B

Đáp án B.
Xác suất để xạ thủ thứ nhất bắn không trúng bia là:![]()
Xác suất để xạ thủ thứ hai bắn không trúng bia là:![]()
Gọi biến cố A:![]() Có ít nhất một xạ thủ không bắn trúng bia
Có ít nhất một xạ thủ không bắn trúng bia![]() . Khi có biến cố A có 3 khả năng xảy ra:
. Khi có biến cố A có 3 khả năng xảy ra:
* Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia là ![]()
* Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia là ![]() .
.
* Xác suất cả hai người đều bắn không trúng bia là ![]() .
.
Vậy ![]() .
.

Đáp án D
Phương pháp:
A, B là các biến cố độc lập thì P(A.B) = P(A).P(B)
Chia bài toán thành các trường hợp:
- Một người bắn trúng và một người bắn không trúng,
- Cả hai người cùng bắn không trúng.
Sau đó áp dụng quy tắc cộng.
Cách giải:
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 2 = 1 2
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 3 = 2 3
Gọi biến cố A:”Có ít nhất một xạ thủ không bắn trúng bia ”.
Khi đó biến cố A có 3 khả năng xảy ra:
+) Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia: 1 2 . 2 3 = 1 3
+) Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia: 1 2 . 1 3 = 1 6
+) Xác suất cả hai người đều bắn không trúng bia:
Khi đó
![]()

Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
P A 1 = 1 2 . 1 − 1 3
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
P A 2 = 1 − 1 2 . 1 3
TH3. Cả 2 xạ thủ đều bắn trượt
P A 3 = 1 − 1 2 . 1 − 1 3
Xác suất của biến cố Y là:
P Y = P A 1 + P A 2 + P A 3 = 5 6
Đáp án. D
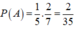
Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ” ⇒ P X = 1 5 .
Gọi Y là biến cố: “người thứ hai ném trúng rổ" ⇒ P Y = 2 7 .
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P ( A ) = P ( X ) . P ( Y ) = 1 5 . 2 7 = 2 35
Chọn đáp án D