Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

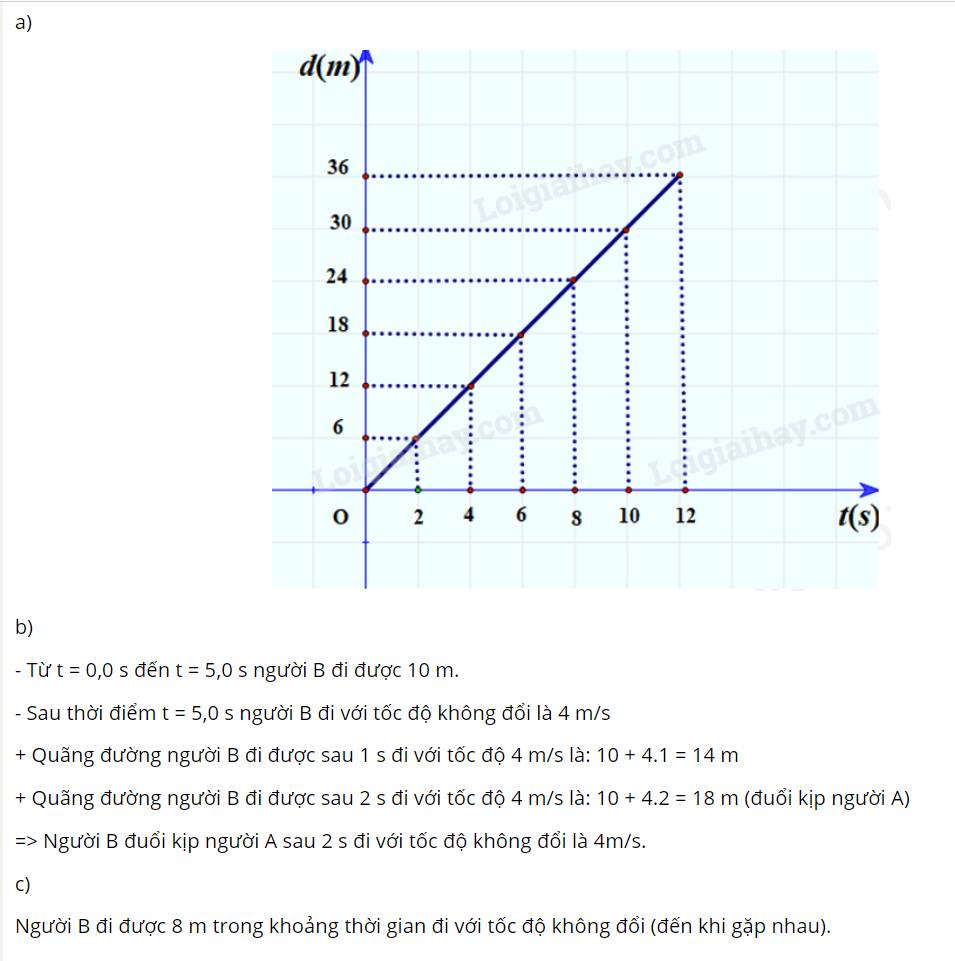
a) Hình lấy từ nguồn khác.
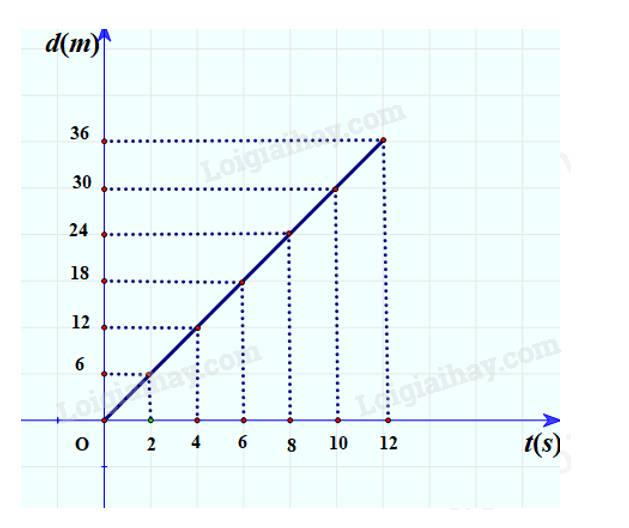
b)
- Từ t = 0,0 s đến t = 5,0 s người B đi được 10 m.
- Sau thời điểm t = 5,0 s người B đi với tốc độ không đổi là 4 m/s
+ Quãng đường người B đi được sau 1 s đi với tốc độ 4 m/s là: 10 + 4.1 = 14 m
+ Quãng đường người B đi được sau 2 s đi với tốc độ 4 m/s là: 10 + 4.2 = 18 m (đuổi kịp người A)
=> Người B đuổi kịp người A sau 2 s đi với tốc độ không đổi là 4m/s.
c)
Người B đi được 8 m trong khoảng thời gian đi với tốc độ không đổi (đến khi gặp nhau).

1) Lấy A làm gốc tọa độ, gốc thời gian lúc ô tô xuất phát từ A, chiều dương từ A->B
Phương trình chuyển động :
\(X=x_0+vt+v't'=0+30.1+60t'=30+60t'\)
2) Phương trình chuyển động của mỗi người là:
người đi bộ: \(x_1=x_0+vt=4t\)
người đi xe đạp: \(x_2=x_0-20.\left(t-1\right)\)
bạn ơi cho mk hỏi tại sao câu 1 lại có 30.1 vậy? sao ko phải 30.2
câu 2 thì người đi xe đạp đi theo chiều dương và xuất phát từ gốc tọa độ tại sao lại là \(x_0-20\left(t-1\right)\)mà ko phải 20(t-1) vậy?
mk vừa học bài này nên ko hiểu cách suy nghĩ có đúng ko giải thích hộ mk với!

a)
Đổi 72 km/h = 20 m/s
Do xe A chuyển động thẳng đều nên:
Quãng đường xe A đi được trong 10 s đầu tiên là:
s = vA .t = 20 .10 = 200 (m)
b)
Xe B chuyển động nhanh dần đều
Ta có:
v0B = 45 km/h = 12, 5 m/s
vB = 90 km/h = 25 m/s
Gia tốc của xe B trong 10 s đầu tiên là:
\(a = \frac{{{v_B} - {v_{0B}}}}{t} = \frac{{25 - 12,5}}{{10}} = 1,25(m/{s^2})\)
Quãng đường đi được của xe B trong 10 s đầu tiên là:
\(s = \frac{{v_B^2 - v_{0B}^2}}{{2.a}} = \frac{{{{25}^2} - 12,{5^2}}}{{2.1,25}} = 187,5(m)\)
c)
Chọn gốc tọa độ tại vị trí xe A bắt đầu vượt xe B, chiều dương là chiều chuyển động của 2 xe, mốc thời gian tại thời điểm xe A bắt đầu vượt xe B
Phương trình chuyển động của 2 xe là:
+ Xe A: \({x_A} = {x_{0A}} + {v_A}.t = 0 + 20.t = 20t\)
+ Xe B: \({x_B} = {x_{0B}} + {v_{0B}}.t + \frac{1}{2}a{t^2} = 0 + 12,5.t + \frac{1}{2}.1,25.{t^2} = 12,5t + 0,625{t^2}\)
Hai xe gặp nhau nên:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 20t = 12,5t + 0,625{t^2}\\ \Leftrightarrow 0,625{t^2} - 7,5t = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 0(L)\\t = 12(TM)\end{array} \right.\end{array}\)
d)
Quãng đường mỗi ô tô đi được kể từ lúc t = 0 đến lúc hai xe gặp nhau là:
s = vA .t = 20 . 12 = 240 (m)

a/Chọn hệ quy chiếu:
- gốc tọa độ tại A
- chiều dương là hướng chuyển động của hai người
- gốc thời gian lúc người đi bộ xuất phát
Phương trình chuyển động của hai người có dạng:
\(\left\{{}\begin{matrix}x_1=x_{01}+v_1.\left(t-t_{01}\right)\\x_2=x_{02}+v_2.\left(t-t_{02}\right)\end{matrix}\right.\)
Có: \(\left\{{}\begin{matrix}x_{01}=o\left(km\right)\\v_1=4\left(km/h\right)\\t_{01}=o\left(h\right)\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x_{02}=o\left(km\right)\\v_2=12\left(km/h\right)\\t_{02}=1\left(h\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x_1=0+4.\left(t-0\right)\\x_2=0+12.\left(t-1\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x_1=4t\\x_2=12t-12\end{matrix}\right.\)
b/ Khi hai xe gặp nhau ta có: \(x_1=x_2\)
=> 4t = 12t -12
=> t = 1.5 (h)
=> \(x_1=x_2=6\left(km\right)\)
Vậy sau 1.5 giờ 2 người gặp nhau cách gốc 6 km.
c/
* Người đi bộ:
| t | 0 | 1.5 |
| x | 0 | 6 |
* Người đi xe đạp:
| t | 1 | 1.5 |
| x | 0 | 6 |
x(km) 6 4 0 t (h) 0.5 1.5 1 x2 x1