Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x 6cm 4cm Theo định lý Py - ta - go :
x2 = 42 + 62
⇒ x2 = 16 + 36
⇒ x2 = 52
⇒ x = √52 (cm)
Vậy đáp án (B) là chính xác
Nhắc lại : Đáp án (B)

Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là a.
Ta có: a2 = 32 + 32 = 18
Suy ra a = √18
Vậy đường chéo của hình vuông đó bằng 3√2.
b) Gọi cạnh của hình vuông là a.
Ta có a2 + a2 + 22 =>2 a2 = 4 => a2 = 2 => a = √2
Vậy cạnh của hình vuông đó bằng √2
Ta có: a2 = 32 + 32 = 18
Suy ra a = √1818
Vậy đường chéo của hình vuông đó bằng 3√22.
b) Gọi cạnh của hình vuông là a.
Ta có a2 + a2 + 22 =>2 a2 = 4 => a2 = 2 => a = √22
Vậy cạnh của hình vuông đó bằng √22.

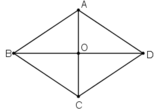
- Gọi ABCD là hình thoi, O là giao điểm hai đường chéo.
⇒ O là trung điểm của AC và BD.
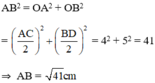
Vậy chọn đáp án là B.

\(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=a^2+b^2+M\)
\(S_{ABCD}\)nhỏ nhất khi M nhỏ nhất
BĐT Cosi \(\left(S_{AOD}+S_{BOC}\right)^2\ge4\cdot S_{AOD}\cdot S_{BOC}\)
\(\Rightarrow\left(\frac{S_{AOD}+S_{BOC}}{2}\right)^2\ge S_{AOD}\cdot S_{BOC}\)(*)
Dấu "=" khi và chỉ khi SAOD=SBOC
Vì \(\Delta\)AOD và \(\Delta\)AOB có chung đường cao kẻ từ A => \(\frac{S_{AOB}}{S_{AOD}}=\frac{OB}{OD}\left(1\right)\)
Tương tự với \(\Delta COD\)và \(\Delta COB\)=> \(\frac{S_{COB}}{S_{COD}}=\frac{OB}{OD}\left(2\right)\)
Từ (1) và (2) => \(\frac{S_{AOB}}{S_{AOD}}=\frac{S_{COB}}{S_{COD}}\)
\(\Rightarrow S_{AOD}\cdot S_{BOC}=S_{AOB}\cdot S_{COD}=a^2b^2\)
Khi đó (*) => \(\left(\frac{S_{AOD}+S_{BOC}}{2}\right)^2\ge a^2b^2\Rightarrow\frac{S_{AOD}+S_{BOC}}{a}\ge2\left|a\right|\left|b\right|\)
\(\Rightarrow S_{ABCD}=a^2+b^2+M\ge a^2+b^2+2\left|a\right|\left|b\right|=\left(\left|a\right|+\left|b\right|\right)^2\)
Vậy SABCD nhỏ nhất =(|a|+|b|)2 <=> SAOD=SBOC
Bài giải:
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB =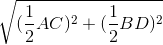
Do đó theo đề bài: AB =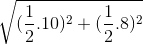
AB =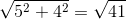
Vậy (B) đúng.
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB =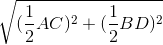
Do đó theo đề bài: AB =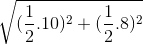
AB =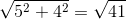
Vậy (B) đúng.