

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a) dễ thấy A,O,B,C cùng thuộc đường tròn đường kính OC
suy ra A,C,B,O,D thuộc đường tròn đường kính OC
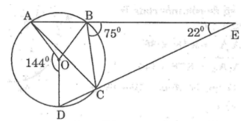
Ta có : \(\widehat{BED}=\widehat{ECB}+\widehat{EBC}=\widehat{BAD}+\widehat{EAB}=\widehat{DAE}\)
b) vì AC = AB nên \(\widebat{AB}=\widebat{AC}\Rightarrow\widehat{ADE}=\widehat{EDB}\)
Xét \(\Delta ADE\)và \(\Delta EDB\)có :
\(\widehat{ADE}=\widehat{EDB}\); \(\widehat{DAE}=\widehat{BED}\)
\(\Rightarrow\Delta ADE~\Delta EDB\left(g.g\right)\Rightarrow\frac{AD}{DE}=\frac{ED}{BD}\Rightarrow DE^2=AD.BD\)

A B M C N D O E
a) Ta có : \(\widehat{ANC}=\widehat{ACM}=\frac{1}{2}\) sđ cung MC ; Góc CAN là góc chung của hai tam giác CAM và tam giác NAC
\(\Rightarrow\Delta CAM~\Delta NAC\left(g.g\right)\) \(\Rightarrow\frac{CM}{CN}=\frac{AC}{AN}\) (1)
Tương tự với tam giác BAM và tam giác NAB ta cũng có \(\widehat{MBA}=\widehat{ANB}=\frac{1}{2}\)sđ cung BM ; Góc NAB là góc chung của hai tam giác
\(\Rightarrow\Delta BAM~\Delta NAB\left(g.g\right)\Rightarrow\frac{AB}{AN}=\frac{BM}{BN}\) (2)
Mà AB = AC (vì AB và AB là hai tiếp tuyến của (O))
Do đó, kết hợp (1) và (2) ta có \(\frac{CM}{CN}=\frac{BM}{BN}\Rightarrow BM.CN=BN.CM\)

a gọi I là trung điểm của A=> I thuộc đường tròn (O) vì OI-1/2.)OA=1.2.2R=R= BK
có AB,AC là tiếp tuyến của (O)
=>góc ABO=góc ACO=90 độ
=> tam giác ABO vuông tại B, có BI là đường trung tuyến
=> BI=OI=IA
có OI=OC=OB
=> tứ giác OBIC là hình thoi
=> OI là đường phân giác của góc BIC(tính chất hình thoi) hay AI là phân giác góc BAC(1)
lại có ABOC nội tiếp(O) (cmt)
=> AO vuông góc với BC hay AI vuông góc với BC(2), AB=AC(3)
từ (1)(2)(3)=> tam giác ABC đều
O A B C D E
a) Ta thấy ngay \(\widehat{BDA}=\widehat{CBA}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cung cùng chắn một cung)
Vậy nên \(\Delta ABC\sim\Delta ADB\left(g-g\right)\)
b) Do \(\Delta ABC\sim\Delta ADB\Rightarrow\frac{AB}{AD}=\frac{AC}{AB}\Rightarrow AB^2=AD.AC\)
Xét tam giác vuông OBA có \(AB=\sqrt{AO^2-OB^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
Vậy nên \(AD.AC=AB^2=3R^2\)
c) Ta thấy rằng \(\Delta ABC\sim\Delta ADB\Rightarrow\widehat{ABC}=\widehat{ADB}\)
Vậy thì \(\widehat{BEA}=\widehat{DBE}+\widehat{BDE}=\widehat{ABC}+\widehat{CBE}=\widehat{ABE}\)
Suy ra tam giác ABE cân tại A hay AB = AE.
Do A, B cố định nên AE không đổi.
Vậy khi cát tuyến ACD quay xung quanh A thì E di chuyển trên đường tròn tâm A, bán kính AB.
d) Ta có AC.AD = 3R2 ; AC + AD = 7R/2
nên ta có phương trình \(AC\left(\frac{7R}{2}-AC\right)=3R^2\)
\(\Leftrightarrow AC^2-\frac{7R}{2}AC+3R^2=0\Leftrightarrow AC=2R\)
\(\Rightarrow AD=\frac{3R}{2}\)