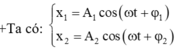
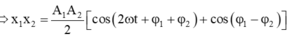
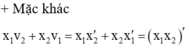
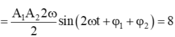
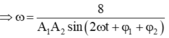
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
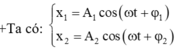
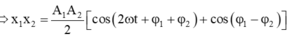
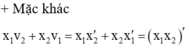
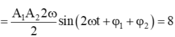
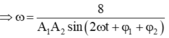
\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)
Đáp án A
Nhìn vào đồ thị ta có:
nên 
.
Tại thời điểm t hai con lắc đơn có cùng li độ và đúng bằng biên độ của con lắc thứ hai nên
.
Tại thời điểm t1 khoảng cách của hai vật theo phương Ox là lớn nhất.
Khi đó từ thời điểm t đến thời điểm t1 vật quay một góc π 2 r a d .
Nên động năng của con lắc thứ hai tại thời điểm t1 là:
.
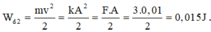Chọn A
+ Cách 1:
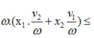
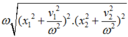
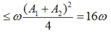
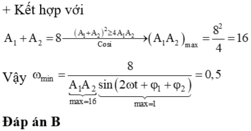
Vậy 
+ Cách 2: Dễ đoán ra dấu “= “ xảy ra khi A1 = A2 = 4cm => x1 cùng pha x2. Vì biểu thức trên kia đúng với mọi thời điểm nên lấy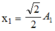 
để thử => Đáp án A.
Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)
Đáp án A
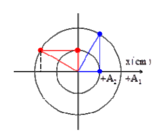
Từ hình vẽ ta thu thập được: F 1 = - 100 x F 2 = - 300 x v à A 1 = 2 A 2 = 1
Khoảng cách giửa hai dao động là lớn nhất khi (l)(2)vuông góc với phương thăng đứng
Tại vị trí này ta thấy rang vật (2) đang có động năng cực đại bang cơ năng, vật 1 đang ở vị trí
chọn A
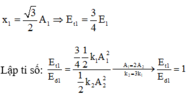
Đáp án D
Theo giả thiết bài toán, ta có:
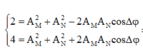
Áp dụng bất đẳng thức Bunhia cho biểu thức trên
