Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Nhận xét: Thay t =0 vào phương trình vận tốc: v = 4\(\pi\) = vmax
Do vận tốc đạt cực đại, nên vật qua VTCB, nên x = 0.
ta có PT chuẩn: x=Acos(wt+fi); v=-wAsin(wt+fi) => v=wAcos(wt+fi) cụ thể v=4picos(2pit+fi0) hay v=4picos2pit => A=2 mà fi=0 => x được chọn là x=2

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Độ cứng của lò xo là:
\(k=\frac{2W}{A^2}=\frac{2X0,2}{0,1^2}=40\left(N/m\right)\)
Tần số góc là:
\(\omega=\frac{2\pi}{T}=\frac{2\pi}{0,5}=4\left(rad/s\right)\)
Khối lượng của vật là:
\(m=\frac{k}{\omega^2}=\frac{40}{\left(4\pi\right)^2}=0,25\left(kg\right)=250\left(g\right)\)
 chọn A
chọn A
Chọn đáp án B
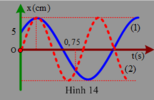
+ Từ đồ thị:
+ Lại có: 0 , 75 = T 1 2 ⇒ T 1 = 1 , 5 s
+ Ta lại có:
Tại: t = 0,75s ⇒ x = A c o s ( ω 2 t - π 2 )
⇒ x = A c o s ( 7 π 3 . 0 , 75 - π 2 ) = - A 2
= x 1 = - 5 c m ⇒ A = 5 2 c m
Suy ra: v m a x = ω 1 A = 4 3 . π 5 2 = 29 , 62 c m / s