Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

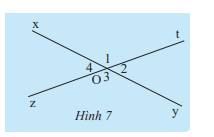
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

a)
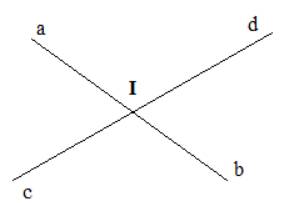
Các cặp góc đối đỉnh trên hình vẽ là: \(\widehat {aId}\) và \(\widehat {bIc}\); \(\widehat {aIc}\) và \(\widehat {bId}\)
b)
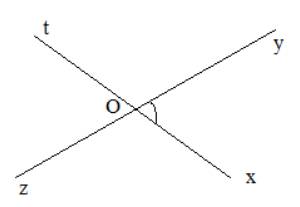
Bước 1: Vẽ góc \(\widehat {xOy}\)
Bước 2: Vẽ tia Ot là tia đối của tia Ox
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
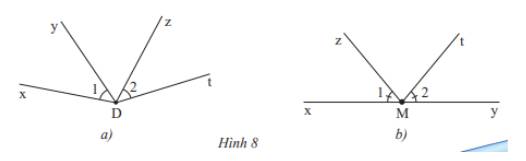
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy
Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

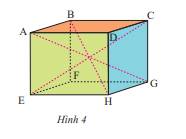
- Các góc ở đỉnh F là: góc BFE, góc BFG, góc EFG
- Các đường chéo được vẽ trong hình là: BH, AG, CE.
- Đường chéo chưa được vẽ là: DF

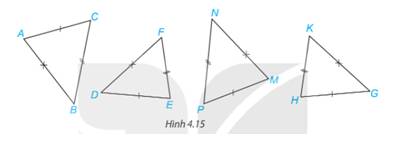
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

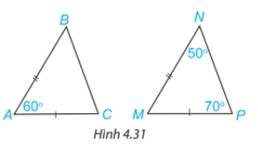
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Ba góc tại mỗi đỉnh chung của ba tam giác tạo thành góc bẹt
Do đó, tổng của chúng bằng 180 độ.
Ta thấy ba điểm A, B, C thẳng hàng.

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
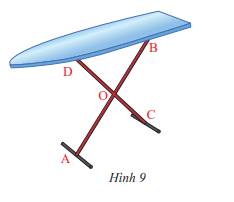





Các góc đối đỉnh trong hình là: \(\widehat {DOB}\) và \(\widehat {COA}\); \(\widehat {BOC}\) và \(\widehat {AOD}\)