Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
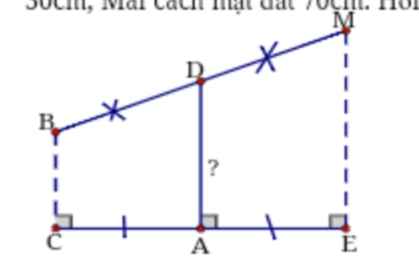
An và Nhiên rủ nhau ra công viên chơi bập bênh. Biết chiều cao của trụ là 50cm. Khi An cách mặt đất 30cm thì Nhiên cách mặt đất bao nhiêu cm? (I,K lần lượt là trung điểm của CB và AD)
#Hỏi cộng đồng OLM
#Toán lớp 8

Nhiên cách mặt đất \(\sqrt{50^2-30^2}=40\left(cm\right)\)

Tham khảo:
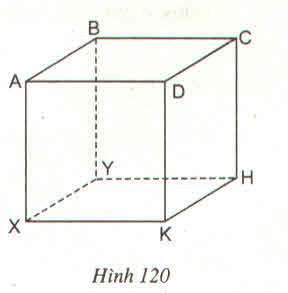
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
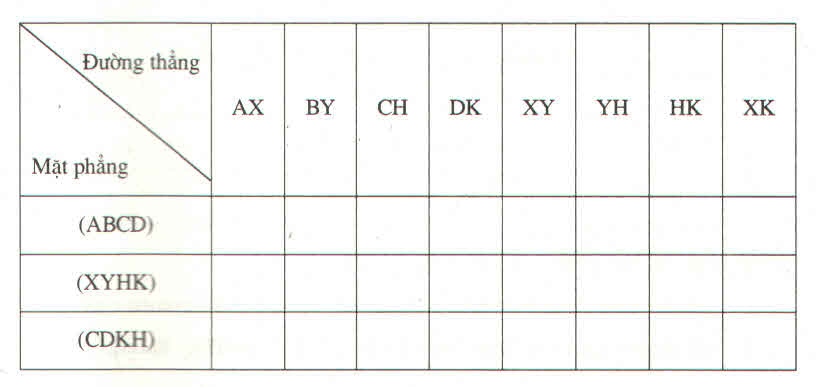
d: 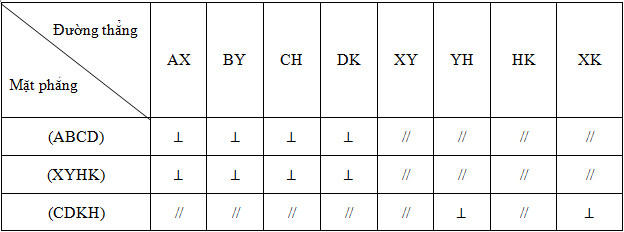

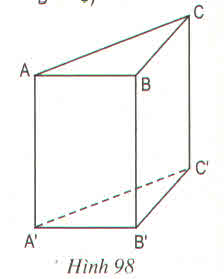
a) Những cặp mặt phẳng song song nhau: (ABC) // (A'B'C')
b) Những cặp mặt phẳng vuông góc với nhau: (ABB'A') ⊥ (A'B'C); (ACC'A') ⊥ (A'B'C'); (BCC'B') ⊥ (A'B'C); (ABB'A') ⊥ (ABC); (ACC'A') ⊥ (ABC); (BCC'B') ⊥ (ABC)
c) Điền vào ô trống:

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.





50 cm