K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 8 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)
DH
23 tháng 8 2019
B=1.2.3+2.3.4+.........+(n−1)n(n+1)B=1.2.3+2.3.4+.........+(n−1)n(n+1)
⇔4B=1.2.3.4+2.3.4.4+........+(n−1)n(n+1).4⇔4B=1.2.3.4+2.3.4.4+........+(n−1)n(n+1).4
⇔4B=(4−0).1.2.3+(5−1).2.3.4+.........+[(n+2)−(n−2)](n−1)n(n+1)⇔4B=(4−0).1.2.3+(5−1).2.3.4+.........+[(n+2)−(n−2)](n−1)n(n+1)
⇔4B=1.2.3.4−0.1.2.3+2.3.4.5−1.2.3.4+.......+(n−1)n(n+1)(n+2)(n+3)−(n−2)(n−1)n(n+1)⇔4B=1.2.3.4−0.1.2.3+2.3.4.5−1.2.3.4+.......+(n−1)n(n+1)(n+2)(n+3)−(n−2)(n−1)n(n+1)
⇔4B=(n−1)n(n+1)(n+2)⇔4B=(n−1)n(n+1)(n+2)
⇔B=(n−1)n(n+1)(n+2)4
2 tháng 6 2020
P(x) = x4 + x2 + 1
Ta có: x4 \(\ge\) 0 với mọi x (Vì số mũ dương)
x2 \(\ge\) 0 với mọi x (Vì số mũ dương)
\(\Rightarrow\) x4 + x2 + 1 \(\ge\) 1 > 0 với mọi x (đpcm)
Chúc bn học tốt! (Phần trong ngoặc là thêm vào cho dễ hiểu thôi!!)
T
0
2 tháng 7 2022
a: Đặt A(x)=0
=>x2(x-1)=0
=>x=0 hoặc x=1
b: Đặt B(x)=0
=>2x+1-1/2x+1=0
=>3/2x=-2
hay x=-2:3/2=-4/3
c: \(3x^2+12\ge12>0\)
nên M(x) vô nghiệm
e: Đặt N(x)=0
=>(x-2)(x-4)=0
=>x=2 hoặc x=4
30 tháng 3 2020
Ta có: \(BD=CE\)
\(\Leftrightarrow BD^2=CE^2\)(1)
Áp dụng định lí pytago vào ΔACE vuông cân tại A, ta được
\(CE^2=AC^2+AE^2\)
hay \(CE^2=2\cdot AC^2\)(2)
Áp dụng định lí pytago vào ΔADB vuông cân tại A, ta được
\(BD^2=AB^2+AD^2\)
hay \(BD^2=2\cdot AB^2\)(3)
Từ (1), (2) và (3) suy ra AB=AC
hay ΔABC cân tại A(định nghĩa tam giác cân)
19 tháng 10 2021
\(=\dfrac{3^6\cdot2^{15}}{2^6\cdot3^6\cdot2^{15}}+\dfrac{12^4}{12^2}=\dfrac{1}{64}+12^2=\dfrac{1}{64}+144=\dfrac{9217}{64}\)
19 tháng 10 2021
\(\dfrac{27^2\cdot8^5}{6^6\cdot32^3}+\dfrac{3^4\cdot4^4}{2^2\cdot6^2}\)
\(=\dfrac{3^6\cdot2^{15}}{3^6\cdot2^6\cdot2^{15}}+\dfrac{3^4\cdot2^8}{2^4\cdot3^2}\)
\(=\dfrac{1}{2^6}+3^2\cdot2^4\)
\(=\dfrac{9217}{64}\)
W
27 tháng 2 2020
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{x+y}{2+3}=\frac{10}{5}=2\)
Suy ra: \(\hept{\begin{cases}a=2\cdot2=4\\b=2\cdot3=6\end{cases}}\)
Vậy a=4,b=6
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
26 tháng 9 2017
\(\left|x\left(x-4\right)\right|=x\)
\(\Rightarrow x\left(x-4\right)=\pm x\)
\(x\left(x-4\right)=x\) hoặc \(x\left(x-4\right)=-x\)
\(x-4=x:x\) \(x-4=-x:x\)
\(x-4=1\) \(x-4=-1\)
\(x=1+4\) \(x=-1+4\)
\(\Rightarrow x=5\) \(\Rightarrow x=3\)
Vậy x=5 hoặc x=3
nhớ tick cho mình nha
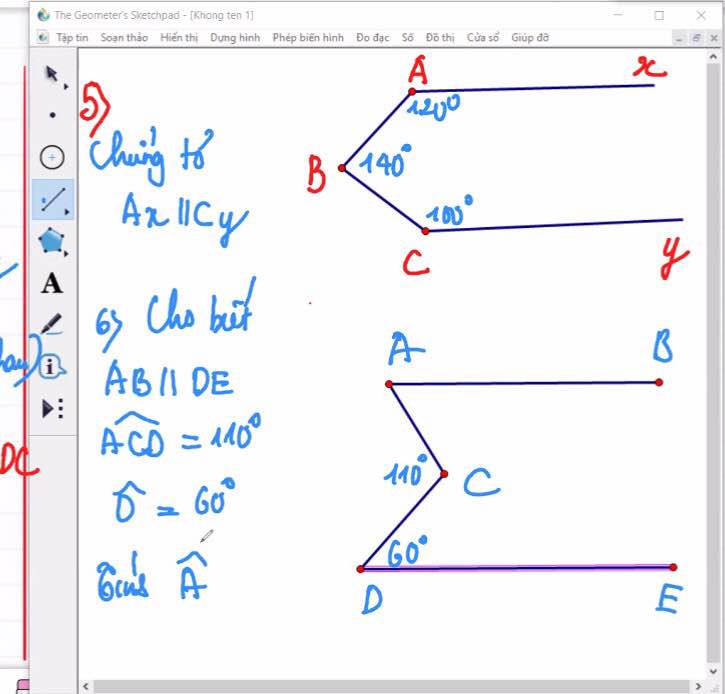
đ
Dề đây ạ
a, \(B=-\left(x+\frac{18}{1273}\right)-\frac{183}{121}\le-\frac{183}{121}\)
Dấu ''='' xảy ra khi \(x=-\frac{18}{1273}\)
Vậy GTLN B là -183/121 khi x = -18/1273
b, \(C=\left(x+\frac{1}{3}\right)^2+5\ge5\Rightarrow\frac{1}{\left(x+\frac{1}{3}\right)^2+5}\le\frac{1}{5}\)
Dấu ''='' xảy ra khi x = -1/3
Vậy GTLN của C là 1/5 khi x = -1/3
c, \(D=\left(x-8\right)^2-4\ge-4\Rightarrow\frac{1}{\left(x-8\right)^2-4}\le-\frac{1}{4}\)
Dấu ''='' xảy ra khi x = 8
Vậy GTLN D là -1/4 khi x = 8