Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
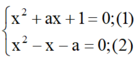
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
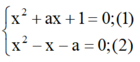
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-

Ta có:
\(\Delta_1+\Delta_2+\Delta_3=a^2-4b+b^2-4c+c^2-4a=a^2+b^2+c^2-48\)
Dễ thấy:\(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=48\Rightarrow\Delta_1+\Delta_2+\Delta_3\ge0\)
Khi đó có ít nhất một phương trình có nghiệm

1) Dùng vi-et rồi phân tích A là ok
2) a) dùng viet , rồi làm sao để khử đc m thông qua S và P là đc
b) pt có 2 nghiệm dương pb : \(\left\{{}\begin{matrix}\Delta>0\\s>0\\p>0\end{matrix}\right.\)
c) 2 nghiem trái dấu : \(\left\{{}\begin{matrix}\Delta\ge0\\p>0\end{matrix}\right.\)
d) cùng âm : \(\left\{{}\begin{matrix}\Delta\ge0\\s< 0\\p>0\end{matrix}\right.\)
e) (x1+x2)2-2x1.x2=x1+x2 ( thay viet vô)
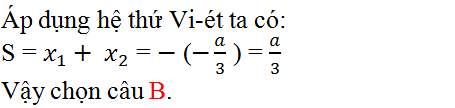
Áp dụng hệ thức Vi-et ta có:
S = x 1 + x 2 = - ( - a / 3 ) = a / 3
Vậy chọn đáp án B