Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2

1) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)

a)\(\Delta'=\left[\frac{-2.\left(m-1\right)}{2}\right]^2-m^2=m^2-2m+1-m^2=-2m+1\)
b)Để PT có hai nghiệm phân biệt thì \(\Delta'=-2m+1>0\Rightarrow m<\frac{1}{2}\)
Để PT có nghiệm kép thì: \(\Delta'=-2m+1=0\Rightarrow m=\frac{1}{2}\)
Để PT vô nghiệm thì: \(\Delta'=-2m+1<0\Rightarrow m>\frac{1}{2}\)

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

1.
đk để pt có nghiệm \(\Delta\)>0 \(\Leftrightarrow\) (-3)2 -4(m-1) >0 \(\Leftrightarrow m< \dfrac{13}{4}\)
theo viet ta có :\(\left\{{}\begin{matrix}x_1+x_2=3\left(1\right)\\x_1\cdot_{ }x_2=m-1\left(2\right)\end{matrix}\right.\)
có 2x1-5x2=-8 (3)
kết hợp (1) , (3) :\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5x_1+5x_2=15\\2x_1-5x_2=-8\end{matrix}\right.\)
cộng vế trên cho vế dưới :7x1=7\(\Rightarrow\)x1=1
có (1) : x1+x2=3 \(\Rightarrow\) x2=3-x1\(\Rightarrow\)x2=3-1=2
thay x1 và x2 vừa tìm đc vào (2) ta đươc \(1\cdot2=m-1\Leftrightarrow m=3\)(tm)
vậy m=3
2. đk để pt có 2 ng dương
\(\left\{{}\begin{matrix}\Delta'\ge0\\S>0\\P>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)^2-4\left(-2m+1\right)\ge0\\x_1+x_2=-2\left(m-2\right)>0\\x_1\cdot x_2=-2m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge0\forall m\\m< 2\\m< \dfrac{1}{ }\end{matrix}\right.\)\(\Leftrightarrow m< \dfrac{1}{2}\) = 0,5
vậy m < 0,5

2/
Xét pt (1) có:
\(\Delta=4\left(m-2\right)^2-4.\left(-2m+1\right)\)
= \(4m^2-8m+12\)
= \(\left(2m-2\right)^2+8\)
Ta có: \(\left(2m-2\right)^2\ge0\) với mọi m
\(\Rightarrow\left(2m-2\right)^2+8>0\) với mọi m
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt với mọi m
Áp ụng hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=4-2m\\x_1.x_2=1-2m\end{matrix}\right.\)
Để pt có 2 nghiệm dương \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1.x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4-2m>0\\1-2m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow m< \dfrac{1}{2}\)
Vậy với \(m< \dfrac{1}{2}\) thì pt đã cho có 2 nghiệm dương

Bài 1:
\(\Delta=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
=>-4m>-13
hay m<13/4
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-5x_2=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=6\\2x_1-5x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_2=14\\x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2\\x_1=1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-1\)
nên m-1=2
hay m=3
Bài 2:
\(\Delta=\left(2m-4\right)^2-4\cdot\left(-2m+1\right)\)
\(=4m^2-16m+16+8m-4\)
\(=4m^2-8m+12\)
\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Để phương trình có hai nghiệm dương thì \(\left\{{}\begin{matrix}-2\left(m-2\right)>0\\-2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)
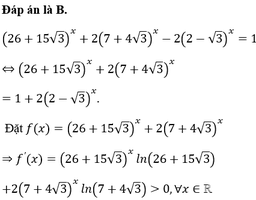


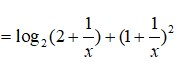
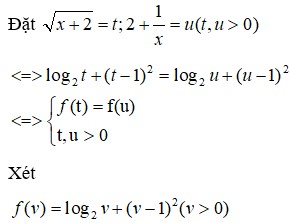
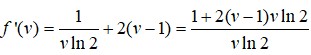

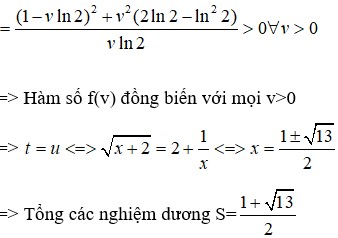
Đáp án A