Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Xét hàm số y =
x
2
-
m
x
+
2
m
x
-
2
trên [-1;1] có: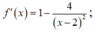 
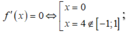
Bảng biến thiên
Trường hợp 1. 
Khi đó
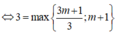
Trường hợp 2. 
Khả năng 1.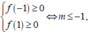 
Khi đó 
Khả năng 2 
Khi đó 
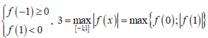
Trường hợp này vô nghiệm.
Khả năng 3. 
Khi đó 
Vô nghiệm.
Vậy có hai giá trị thỏa mãn là 
Do đó tổng tất cả các phần tử của S là -1.
Chọn A
Xét hàm số g(x) =
x
3
-
3
x
2
+
m
có 
Xét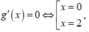 
Khi đó giá trị lớn nhất của hàm số y = | x 3 - 3 x 2 + m | trên [-2;4] là:
Trường hợp 1: Giả sử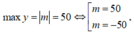 
Với m = 50 thì |m + 16| = 66 > 50 (loại)
Với m = -50 thì |m - 20| = 70 > 50 (loại)
Trường hợp 2: Giả sử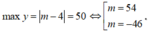 
Với m = 54 => |m| = 54 > 50 (loại)
Với m = -46 thì |m - 20| = 66 > 50 (loại)
Trường hợp 3: Giả sử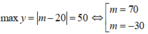 
Với m = 70 thì |m + 16| = 86 > 50 (loại)
Với m = -30 thì |m + 16| = 14 < 50, 
(thỏa mãn)
Trường hợp 4: Giả sử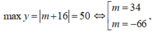 
Với m = 34 thì |m| = 34 < 50, 
(thỏa mãn)
Với m = -66 thì |m| = 66 > 50 (loại)
Vậy 
Do đó tổng các phẩn tử của S là: -30 + 34 = 4.
Chọn A
Kiến thức bổ sung: Dạng toán tìm GTLN, GTNN của hàm số y = |u(x)| trên đoạn [a;b]
Gọi M, m lần lượt là GTLN, GTNN của hàm số u(x) trên đoạn [a;b]
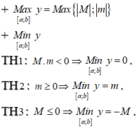
Đặt: 
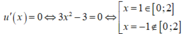
Ta có: 
Suy ra: 
TH1: 
(loại)
(vì ko thỏa mãn giả thiết Aa = 12)
TH2: 
Từ giả thiết: Aa = 12 
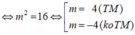
TH3: 
Từ giả thiết: Aa = 12 
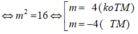
Kết hợp các trường hợp suy ra: S = {-4;4}
Vậy tổng các phần tử của bằng: (-4) + 4 = 0.
Chọn A
Đặt 
ta có: 
Ta có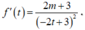 
Do m ∈ Z nên ta xét hai trường hợp sau
+TH1: 
thì hàm số đồng biến trên [-1;1].
Xét 
+TH2: 
thì hàm số nghịch biến trên [-1;1]
Xét 
Vậy 
Vậy tập S có 4 phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]
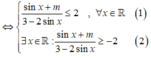
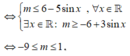
+ Xét hàm số f(x) = x3-3x+ m là hàm số liên tục trên đoạn [0; 2] .
Ta có đạo hàm f’ (x) = 3x2- 3 và f’ (x) = 0 khi x= 1 ( nhận ) hoặc x= -1( loại)
+ Suy ra GTLN và GTNN của f(x) thuộc { f(0); f(1) ; f(2) }={m;m-2; m+2}.
+ Xét hàm số y = x 3 - 3 x + m trên đoạn [0; 2 ] ta được giá trị lớn nhất của y là
m a x m ; m - 2 ; m + 1 = 3 .
TH1: m= 3 thì max {1;3;5}= 5 ( loại )
TH2: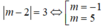 
+ Với m= -1. Ta có max {1; 3}= 3 (nhận).
+Với m= 5. Ta có max { 3;5;7}= 7 (loại).
TH3: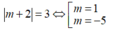 
+ Với m= 1. Ta có max {1; 3}= 3 (nhận).
+ Với m= -5. Ta có max {3;5;7}= 7 (loại).
Do đó m= -1 hoặc m= 1
Vậy tập hợp S có phần tử.
Chọn B.
Chọn D.
Cách 1. Xét hàm số y = f(x)
x
3
-
3
x
2
-
9
x
+
m
có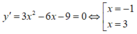 
Ta có bảng biến thiên sau
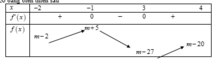
Giá trị lớn nhất của hàm số y = | x 3 - 3 x 2 - 9 x + m | trên đoạn bằng 16 khi và chỉ khi
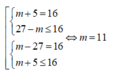
Vậy m = 11 là giá trị duy nhất của thỏa mãn
Cách 2: Xét hàm số y = f(x) = x 3 - 3 x 2 - 9 x + m có
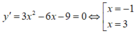
Ta có: 
Vậy 
Xét phương trình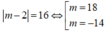 
không có giá trị nào của thỏa mãn vì
m = 18 thì 
m = -14 thì 
Xét phương trình 
không có giá trị nào của thỏa mãn vì
m = 36 thì 
m = 4 thì 
Xét phương trình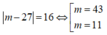 
có một giá trị thỏa mãn vì
m = 43 thì 
m = 11 thì 
(thỏa mãn)
Xét phương trình 
có một giá trị thỏa mãn vì
m = 11 thì 
(thỏa mãn)
m = -21 thì 
Vậy có m = 11 thỏa mãn yêu cầu bài toán.
Chọn D.
Cách 1. Xét hàm số y = f(x)
x
3
-
3
x
2
-
9
x
+
m
có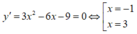 
Ta có bảng biến thiên sau
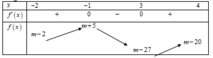
Giá trị lớn nhất của hàm số y = | x 3 - 3 x 2 - 9 x + m | trên đoạn bằng 16 khi và chỉ khi
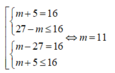
Vậy m = 11 là giá trị duy nhất của thỏa mãn
Cách 2: Xét hàm số y = f(x) = x 3 - 3 x 2 - 9 x + m có
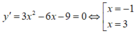
Ta có: 
Vậy 
Xét phương trình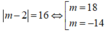 
không có giá trị nào của thỏa mãn vì
m = 18 thì 
m = -14 thì 
Xét phương trình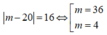 
không có giá trị nào của thỏa mãn vì
m = 36 thì 
m = 4 thì 
Xét phương trình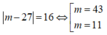 
có một giá trị thỏa mãn vì
m = 43 thì 
m = 11 thì 
(thỏa mãn)
Xét phương trình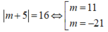 
có một giá trị thỏa mãn vì
m = 11 thì 
(thỏa mãn)
m = -21 thì 
Vậy có m = 11 thỏa mãn yêu cầu bài toán.
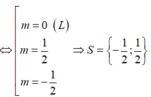
Vậy tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là 1.
Chọn C
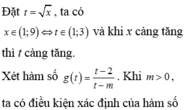
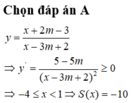
*Đặt \(f\left(x\right)=x^2+x-m.\)Ta có: \(f'\left(x\right)=2x+1\)
\(f'\left(x\right)=0\Leftrightarrow x=-\frac{1}{2}\)
Bảng biến thiên (nguồn: Moon.vn)
*Trường hợp 1:\(-m-\frac{1}{4}>0\Leftrightarrow m< -\frac{1}{4}\)
Ta có:
\(min\)\(f\left(x\right)=-m-1\Rightarrow min\)\(y=\left(-m-\frac{1}{4}\right)^2=4\)
\(x\in\left[-2;2\right]\) \(x\left[-2;2\right]\)
\(\Leftrightarrow\orbr{\begin{cases}m=-\frac{9}{4}\left(n\right)\\m=\frac{7}{4}\left(l\right)\end{cases}}\)
*Trường hợp 2: \(-m+6< 0\Leftrightarrow m>6\)
Ta có
\(min\)\(f\left(x\right)=-m-1\Rightarrow min\)\(y=\left(-m+6\right)^2=4\)
\(x\in\left[-2;2\right]\) \(x\in\left[-2;2\right]\)
\(\Leftrightarrow\orbr{\begin{cases}m=4\left(l\right)\\m=8\left(n\right)\end{cases}}\)
*Trường hợp 3:
\(-m-1\)≤\(0\)≤\(-m+6\Leftrightarrow-\frac{1}{4}\)≤\(m\)≤\(6\)
Ta có \(min\)\(f\left(x\right)=0\Rightarrow min\)\(y=0\). Suy ra\(-\frac{1}{4}\)≤\(m\)≤\(6\)
(điều kiện tương tự như mấy câu trên, tui lười viết kí hiệu lắm)
Không thỏa mãn yêu cầu đề bài
\(Vậy\)\(m\in\left\{-\frac{9}{4};8\right\}\Rightarrow S=\frac{23}{4}\)
Pls tiick tui, tui đã ngồi 1 tiếng để giải bài này TvT
Hok tốt