Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua O vẽ OH ⊥ AB và OK ⊥ AD ⇒ OH ⊥ DC, OK ⊥ BC
Gọi I, L lần lượt là giao điểm của OK, OH với DC, BC. Ta có:
+ S_ABCD = AB.IH = BC.KL
+ S_ABO = 1/2 AB.OH và S_CDO = 1/2 DC.OI
⇒ S_ABO + S_CDO = 1/2 AB.OH + 1/2 DC.OI
= 1/2 AB.OH + 1/2 AB.OI
= 1/2 AB (OH + OI) = 1/2 AB.IH = 1/2 S_ABCD (1)
+ S_BCO = 1/2 BC.OL và S_DAO = 1/2 AD.OK
⇒ S_BCO + SDAO = 1/2 BC.OL + 1/2AD.OK
= 1/2 BC.OL + 1/2BC.OK
= 1/2BC(OL + OK) = 1/2 BC.KL = 1/2S_ABCD (2)
Từ (1) và (2) ta có: S_ABO + S_CDO = S_BCO + S_DAO

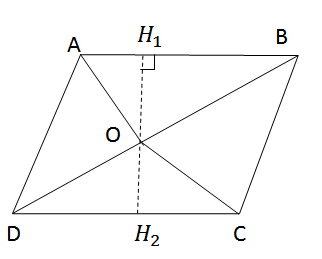
Từ O lẻ đường thẳng d vuông góc với AB ở H1, cắt CD ở H2.
Ta có OH1 ⊥ AB
Mà AB // CD
Nên OH2 ⊥ CD
Do đó: SABO + SCDO = \(\dfrac{1}{2}\)OH1 . AB + \(\dfrac{1}{2}\) OH2 . CD
= \(\dfrac{1}{2}\)AB (OH1 + OH2)
= \(\dfrac{1}{2}\)AB . H1 . H2
Nên \(S_{ABO}+S_{CDO}=\dfrac{1}{2}S_{ABCD}\) ( 1)
Tương tự \(S_{BCO}+S_{DAO}=\dfrac{1}{2}S_{ABCD}\) (2)
Từ (1) và (2) suy ra :
\(S_{ABO}+S_{CDO}=S_{BCO}+S_{DAO}\)

A B C D O E F H K
Ta có SABO = OE.AB : 2
Vì \(\hept{\begin{cases}AB//CD\\\widehat{AEO}=90^{\text{o}}\end{cases}}\Rightarrow\widehat{CFO}=90^{\text{o}}\)
=> SCDO = OF.CD : 2 = OF.AB : 2
=> SABO + SCDO = EF.AB : 2 = \(\frac{1}{2}S_{ABCD}\)(Vì EF là đường cao hình bình hành ABCD => SABCD = EF.AB)
Tương tự ta được
SBCO + SDAO = HK.BC : 2 = \(\frac{1}{2}S_{ABCD}\)(HK đường cao hình bình hành ABCD => SABCD = HK.BC)
=> SABO + SCDO = SBCO + SDAO (= \(\frac{1}{2}S_{ABCD}\)) => ĐPCM

Bạn tự vẽ hình nha
- Nếu O thuộc BD ta hiển nhiên có điều phải chứng minh
- Nếu O không thuộc BD
Giả sử BD cắt OA, OC lần lượt tại E, F
Từ D và B kẻ các đường vuông góc DH, BK xuống AO với H,K thuộc AO
Ta có : \(S_{OAD}=S_{OAB}\)mà hai tam giác này có chung đáy OA ⇒DH=BK
Xét tam giác DHE vuông tại H và tam giác BKE vuông tại K có:
DH=BK
\(\widehat{EDH}=90^o-\widehat{DEH}=90^o-\widehat{BEK}=\widehat{EBK}\)
\(\Rightarrow\Delta EDH=\Delta EBK\)
\(\Rightarrow DE=EB\)
Tương tự \(S_{ODC}=S_{OBC}\Rightarrow DF=FB\)
\(\Rightarrow E\equiv F\)
O, C, F thẳng hàng ; O, E, A thẳng hàng ; E = F ⇒⇒ A, C, O, E thẳng hàng. Vậy O thuộc đường chéo AC.
kuihihuolu uh
| ]o-][[p[po[]\[]iy89t768r67r675r65r67r5676666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666 |

Có:
\(\dfrac{S_{DAO}}{S_{ABO}}=\dfrac{DO}{BO}=\dfrac{S_{CDO}}{S_{BCO}}\) , tức là \(S_{DAO}.S_{BCO}=S_{ABO}.S_{CDO}\)
Do đó:
\(S_{ABO}.S_{BCO}.S_{CDO}.S_{DAO}=\left(S_{DAO}+S_{BCO}\right)^2\)
Vậy tích các số đo diện tích của các tam giác ABO, BCO, CDO, DAO là một số chính phương.
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
Mà SABCD = SAOB + SBOC + SCOD + SDOA
Do đó SAOB + SCOD = SBOC + SDOA.