
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

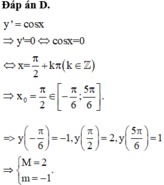

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

\(1-cos^2x+1-cos^2y=\frac{1}{4}\Rightarrow cos^2x+cos^2y=\frac{7}{4}\)
\(\Rightarrow\frac{3}{4}\le cos^2x;cos^2y\le1\)
\(S=1+tan^2x+1+tan^2y-2=\frac{1}{cos^2x}+\frac{1}{cos^2y}-2\)
\(=\frac{7}{4cos^2x.cos^2y}-2=\frac{7}{4cos^2x\left(\frac{7}{4}-cos^2x\right)}-2=\frac{7}{-4cos^4x+7cos^2x}-2\)
Đặt \(cos^2x=t\) \(\Rightarrow\frac{3}{4}\le t\le1\)
Xét \(f\left(t\right)=-4t^2+7t\) trên \(\left[\frac{3}{4};1\right]\)
\(-\frac{b}{2a}=\frac{7}{8}\Rightarrow f\left(\frac{7}{8}\right)=\frac{49}{16}\) ; \(f\left(\frac{3}{4}\right)=3\); \(f\left(1\right)=3\)
\(\Rightarrow3\le f\left(t\right)\le\frac{49}{16}\)
\(\Rightarrow\frac{7}{\frac{49}{16}}-2\le S\le\frac{7}{3}-2\Leftrightarrow\frac{2}{7}\le S\le\frac{1}{3}\)
Không có trong đáp án?

1.
ĐKXĐ: \(\left\{{}\begin{matrix}cos3x\ne0\\tan3x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{6}+\frac{k\pi}{3}\\x\ne\frac{\pi}{12}+\frac{k\pi}{3}\end{matrix}\right.\)
2.
\(-1\le cos\frac{x}{2}\le1\Rightarrow\sqrt{2}\le\sqrt{cos\frac{x}{2}+3}\le2\)
\(\Rightarrow3\sqrt{2}-2\le y\le4\)
3.
a. \(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=sin3x\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=2x-\frac{\pi}{6}+k2\pi\\3x=\frac{7\pi}{6}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b. \(-4\left(1-cos^2x\right)+8\left(1-cosx\right)-1=0\)
\(\Leftrightarrow4cos^2x-8cosx+4=0\)
\(\Leftrightarrow cosx=1\)
\(\Leftrightarrow...\)

\(y=\frac{2cos2x+2+3sin2x+1}{3-sin2x+cos2x}=\frac{2cos2x+3sin2x+3}{3-sin2x+cos2x}\)
\(\Leftrightarrow3y-y.sin2x+y.cos2x=2cos2x+3sin2x+3\)
\(\Leftrightarrow\left(y+3\right)sin2x+\left(2-y\right)cos2x=3y-3\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y+3\right)^2+\left(2-y\right)^2\ge\left(3y-3\right)^2\)
\(\Leftrightarrow7y^2-20y-4\le0\)
\(\Leftrightarrow\frac{10-8\sqrt{2}}{7}\le y\le\frac{10+8\sqrt{2}}{7}\)
\(\Rightarrow\left\{{}\begin{matrix}M=\frac{10+8\sqrt{2}}{7}\\m=\frac{10-8\sqrt{2}}{7}\end{matrix}\right.\) \(\Rightarrow7M-14m=24\sqrt{2}-10\)

Lời giải:
1.
\(y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x\)
\(=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x\)
Vì \(\sin 2x\in [-1;1]\Rightarrow \sin ^22x\in [0;1]\)
Do đó:\(y=1-\frac{1}{2}\sin ^22x\in [\frac{1}{2}; 1]\) hay \(y_{\min}=\frac{1}{2}; y_{\max}=1\)
2.
\(y=\frac{\sin x}{\cos x+2}\Rightarrow y^2=\frac{\sin ^2x}{(\cos x+2)^2}=\frac{1-\cos ^2x}{(\cos x+2)^2}\)
Đặt \(\cos x=t(t\in [-1;1])\) . Xét \(f(t)=\frac{1-t^2}{(t+2)^2}\)
\(f'(t)=\frac{-2(2t+1)}{(t+2)^3}=0\Leftrightarrow t=-\frac{1}{2}\)
Lập BBT ta suy ra \(f(t)_{\max}=f(\frac{-1}{2})=\frac{1}{3}\)
\(\Rightarrow y^2\leq \frac{1}{3}\Rightarrow \frac{-1}{\sqrt{3}}\leq y\leq \frac{1}{\sqrt{3}}\)
Vậy \(y_{\min}=\frac{-1}{\sqrt{3}}; y_{\max}=\frac{1}{\sqrt{3}}\)

Lời giải:
Đặt \(\sin x=t\in [-1;1]\)
Khi đó: \(y=t+\sqrt{2-t^2}\)
\(\Rightarrow y'=1-\frac{t}{\sqrt{2-t^2}}=\frac{\sqrt{2-t^2}-t}{\sqrt{2-t^2}}\)
Có: \(y'=0\Leftrightarrow \sqrt{2-t^2}-t=0\Leftrightarrow t=1\)
Lập bảng biến thiên với các điểm \(t=1, t=-1\) ta thấy hàm số đạt giá trị max tại $t=1$ và min tại $t=-1$. Vậy:
\(y_{\max}=y(1)=1+\sqrt{2-1^2}=2\)
\(y_{\min}=y(-1)=-1+\sqrt{2-(-1)^2}=0\)
tại sao có y' = 1 - \(\dfrac{t}{\sqrt{2-t^2}}\) vậy ạ ?

d/
\(0\le cos^2x\le1\Rightarrow5\le y\le8\)
\(y_{min}=5\) khi \(cosx=0\)
\(y_{max}=8\) khi \(cosx=\pm1\)
e/
\(0\le\left|cos2x\right|\le1\)
\(\Rightarrow-2\le y\le1\)
\(y_{min}=-2\) khi \(cos2x=\pm1\)
\(y_{max}=1\) khi \(cos2x=0\)
f/
\(0\le sin^23x\le1\Rightarrow\sqrt{3}-2\le y\le0\)
\(y_{min}=\sqrt{3}-2\) khi \(sin2x=0\)
\(y_{max}=0\) khi \(sin2x=\pm1\)
a/ \(-1\le sin2x\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin2x=1\)
\(y_{max}=5\) khi \(sin2x=-1\)
b/ \(-1\le cos\left(x-\frac{\pi}{3}\right)\le1\Rightarrow-3\le y\le5\)
\(y_{min}=-3\) khi \(cos\left(x-\frac{\pi}{3}\right)=-1\)
\(y_{max}=5\) khi \(cos\left(x-\frac{\pi}{3}\right)=1\)
c/ \(-1\le cosx\le1\Rightarrow0\le\sqrt{cosx+1}\le\sqrt{2}\)
\(\Rightarrow2\le y\le2+\sqrt{2}\)
\(y_{min}=2\) khi \(cosx=-1\)
\(y_{max}=2+\sqrt{2}\) khi \(cosx=1\)