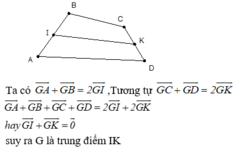
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Vì AM<ÂN
nên điểm M nằm giữa hai điểm A và N
b: MN=AN-AM=5cm
c: PM=PA+AM=3+2=5cm
d: VìMP=MN
và P,M,N thẳng hàng
nên M là trung điểm của PN

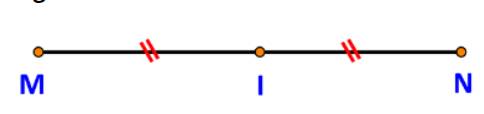
a) Các vectơ đó là: \(\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM} \).
b) Dễ thấy:
+) vectơ \(\overrightarrow {IN} \)cùng hướng với vectơ \(\overrightarrow {MI} \). Hơn nữa: \(|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |\)
\( \Rightarrow \overrightarrow {IN} = \overrightarrow {MI} \)
+) vectơ \(\overrightarrow {IM} \)cùng hướng với vectơ \(\overrightarrow {NI} \). Hơn nữa: \(|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |\)
\( \Rightarrow \overrightarrow {IM} = \overrightarrow {NI} \)
Vậy \(\overrightarrow {IN} = \overrightarrow {MI} \) và \(\overrightarrow {IM} = \overrightarrow {NI} \).

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp(1)
b: Xét tứ giác OEAC có
\(\widehat{OEA}+\widehat{OCA}=180^0\)
Do đó: OEAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,E,B,A,C cùng thuộc một đường tròn
c: \(\widehat{BIC}=\dfrac{sđ\stackrel\frown{BC}}{2}=\dfrac{\widehat{BOC}}{2}\)
mà \(\widehat{AOC}=\dfrac{\widehat{BOC}}{2}\)
nên \(\widehat{BIC}=\widehat{AOC}\)

Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C