Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức : 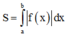
Cách giải: Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k
![]()
Cho 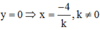 . Vậy, d cắt Ox tại điểm
. Vậy, d cắt Ox tại điểm 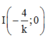
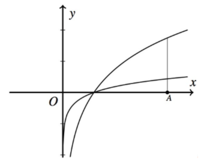
Giao điểm của y = x 2 - 4 x + 4 và trục hoành: Cho y = 0 => x = 2
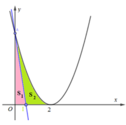
=>Để d chia (H) thành 2 phần thì 
Vì d chia (H) thành 2 phần có diện tích bằng nhau
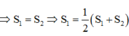
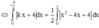
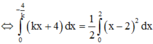
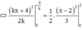
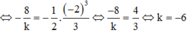

Đáp án A
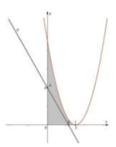
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
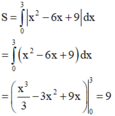
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
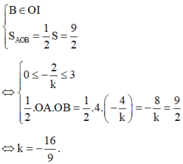 .
.

Đáp án A
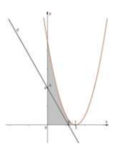
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
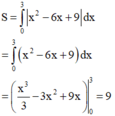
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
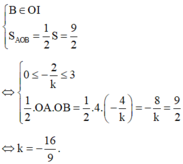

Đáp án A
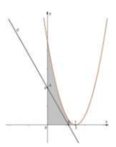
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
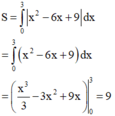
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
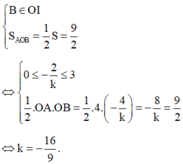

Theo giả thiết và công thức tích phân từng phần, ta có:
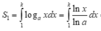
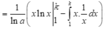
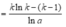
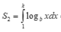
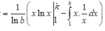
![]()
Vậy ![]()
![]()
Chọn đáp án A.

Đáp án A
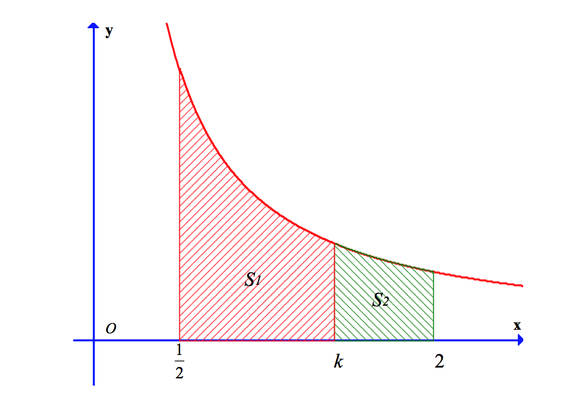
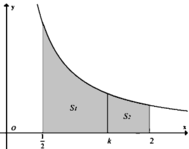
Diện tích hình thang cong (H) là:
S = ∫ 1 2 2 1 x d x = ln x 1 2 2 = ln 4
S 1 = 3 S 2 ⇒ S 2 = S 4 ⇔ ln 4 4 = ln 4 4 = ∫ k 2 1 x d x = ln x k 2 = ln 2 k ⇔ 4 4 = 2 k ⇔ k = 2

Ta có
S 1 = ∫ 0 k e x sin x d x ; S 2 = ∫ k π e x sin x d x S = S 1 + S 2 = ∫ 0 π e x sin x d x
2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2
⇔ S 2 = 2 S 1 2 - 2 S 1 + 1 - S = 0 ⇔ 2 ∫ 0 k e x sin x d x 2 - 2 ∫ 0 k e x sin x d x + 1 - ∫ 0 k e x sin x d x = 0
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án cần chọn là B
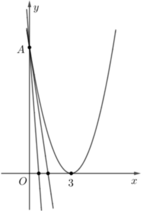
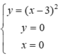
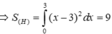
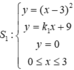
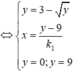
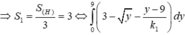
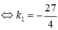
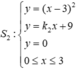
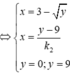
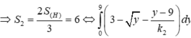
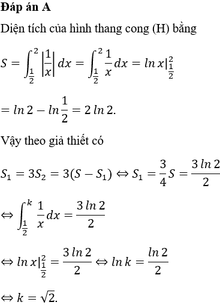
Đáp án D