Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

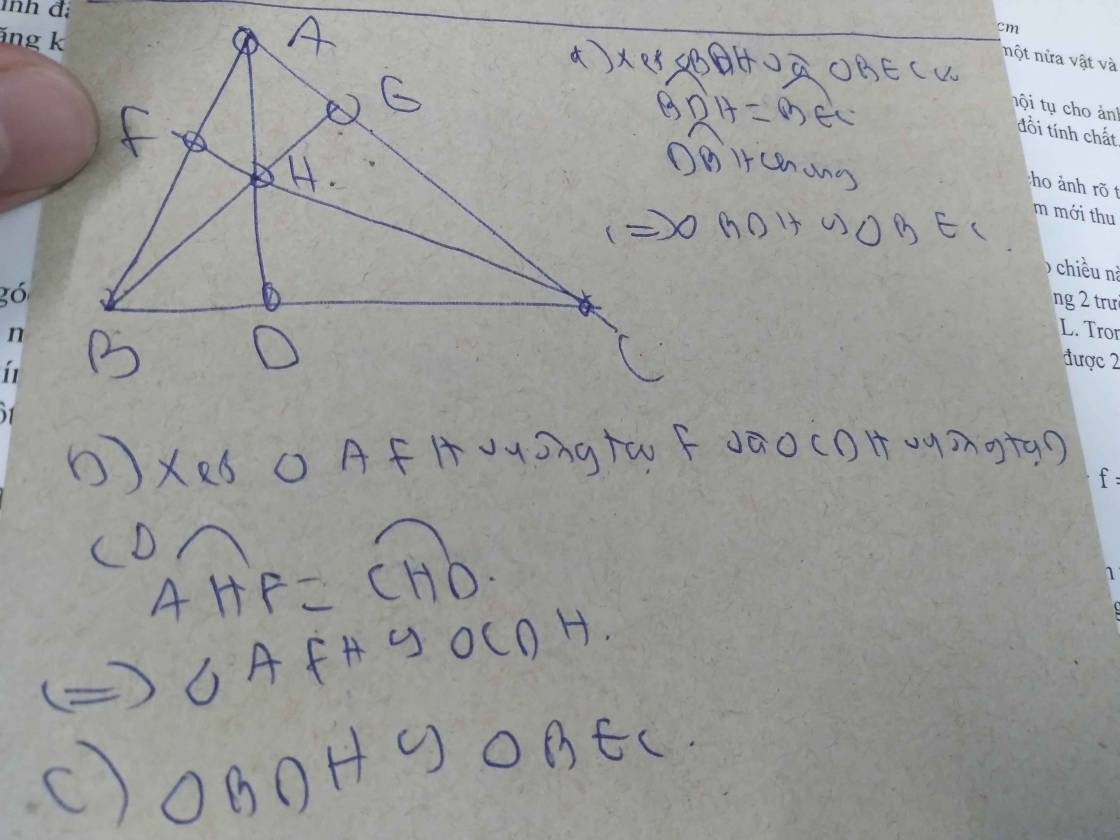
a/Ta có: \(\widehat{BAD}=\widehat{BCH}\)( cùng phụ góc B)
Vậy \(\Delta ADB\sim\Delta CDH\left(g-g\right)\)(1)
b/Từ (1) có: \(\frac{AD}{CD}=\frac{DB}{DH}\Rightarrow AD.DH=CD.BD\le\frac{\left(CD+BD\right)^2}{4}=\frac{9}{4}\)

Mink chứng mink từng câu nha nhưng phần dễ sẽ làm hơi tắt nên bn đọc kĩ nha
a, Xét tam giác ADB và tam giác AEC có
Góc ADB = Góc AEC ( = 90 )
Góc BAC chung
Suy ra tam giác ADB đồng dạng với tam giác AEC ( g.g )
b ,
Có tam giác ADB đồng dạng với tam giác AEC ( c.m.t )
AD/AE = AB/AC ( định nghĩa 2 tam giác đồng dạng )
hay AD/AB = AE/AC
Xét tam giác AED và tam giác ACB có
BAC chung
AD/AB = AE/AC ( c.m.t)
Suy ra tam giác AED đồng dạng với tam giác ACB ( g.g )

a,
Ta có ON // BH ( cùng vuông góc với AC )
OM // AH ( cùng vuông góc với BC )
MN // AB ( MN là đường trung bình của tam giác ABC )
Vậy tam giác OMN đồng dạng với tam giác HAB.
b,
Xét tam giác AHG và MOG có :
\(+,\widehat{HAG}=\widehat{OMG}\)( Do AH // OM )
\(+,\frac{OM}{AH}=\frac{MN}{AB}=\frac{1}{2}=\frac{GM}{GA}\)( DO 2 TAM GIÁC ĐỒNG DẠNG Ở CÂU a, )
Từ đó ta có tam giác AHG đồng dạng với tam giác MOG(c.g.c) nên \(\frac{OG}{HG}=\frac{MG}{MA}=\frac{1}{2}\)
Và \(\widehat{HGO}=\widehat{HGA}+\widehat{AGO}=\widehat{OGM}+\widehat{AGO}=\widehat{AGM}=180^0\)
\(\Rightarrow H,G,O\)thẳng hàng

Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,
ghghhggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh

a, Xét tgABE và tgACF có:
góc AEB = góc CFA = 90o
góc BAC chung
Từ 2 điều trên => tgABE đồng dạng tgACF (g.g)
=> AB/AC = AE/AF (các cặp cạnh tương ứng)
=> AB.AF = AC.AE

Xét ΔABD vuông tại D và ΔCHD vuông tại D có
góc BAD=góc HCD
=>ΔABD đồng dạng vớiΔCHD