Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

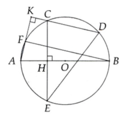
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây

a, Ta có : d(O;AB) = OH
d(O;CD) = OK
AB = CD => OH = OK => EB = ED
mà H ; K lần lượt là trung điểm AB và CD => EH = EK
b, Vi OH = OK => AE = EC

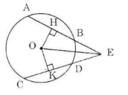
a) Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: OH ⊥ AB
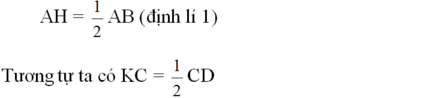
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)
A B C D O H K E
Gọi H,K lần lượt là trung điểm của AB và CD.
Ta có: \(OH\perp AB;OK\perp CD;OH=OK\), Hai dây AB và CD bằng nhau nên khoảng cách đến tâm bằng nhau. Hoặc xét 2 tam giác cân OAB; OCD cân tại O suy ra những điều trên.
Xét 2 tam giác vuông OHE và OKE có: OE chung; OK = OK
Suy ra \(\Delta OHE=\Delta OKE\\ \Rightarrow HE=KE\)
Mặt khác HB = HC => BE = CE
Tương tự ta cũng chứng minh được AE =DE