
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


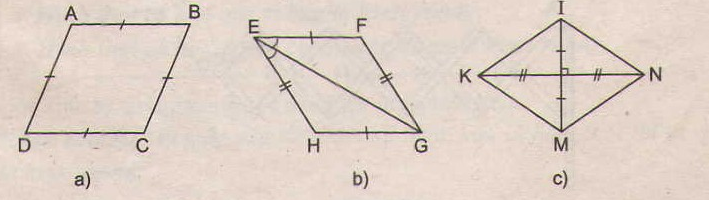
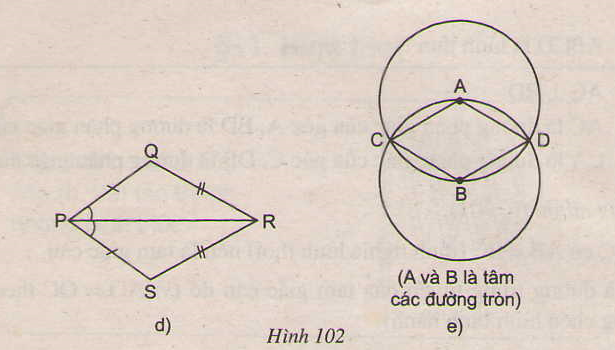
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.

Đề số 3.
1.
a,\(4x\left(5x^2-2x+3\right)\)
\(=20x^3-8x^2+12x\)
b.\(\left(x-2\right)\left(x^2-3x+5\right)\)
\(=x^3-3x^2+5x-2x^2+6x-10\)
\(=x^3-5x^2+11x-10\)
c,\(\left(10x^4-5x^3+3x^2\right):5x^2\)
\(=2x^2-x+\dfrac{3}{5}\)
d,\(\left(x^2-12xy+36y^2\right):\left(x-6y\right)\)
\(=\left(x-6y\right)^2:\left(x-6y\right)\)
\(=x-6y\)
2.
a,\(x^2+5x+5xy+25y\)
\(=\left(x^2+5x\right)+\left(5xy+25y\right)\)
\(=x\left(x+5\right)+5y\left(x+5\right)\)
\(=\left(x+5y\right)\left(x+5\right)\)
b,\(x^2-y^2+14x+49\)
\(=\left(x^2+14x+49\right)-y^2\)
\(=\left(x+7\right)^2-y^2\)
\(=\left(x+7-y\right)\left(x+7+y\right)\)
c,\(x^2-24x-25\)
\(=x^2+25x-x-25\)
\(=\left(x^2-x\right)+\left(25x-25\right)\)
\(=x\left(x-1\right)+25\left(x-1\right)\)
\(=\left(x+25\right)\left(x-1\right)\)
3.
a,\(5x\left(x-3\right)-x+3=0\)
\(5x\left(x-3\right)-\left(x-3\right)=0\)
\(\left(5x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{1}{5}\) hoặc \(x=3\)
b.\(3x\left(x-5\right)-\left(x-1\right)\left(2+3x\right)=30\)
\(3x^2-15x-\left(2x+3x^2-2-3x\right)=30\)
\(3x^2-15x-2x-3x^2+2+3x=30\)
\(-14x+2=30\)
\(-14x=28\)
\(x=-2\)
c,\(\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\)
\(x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\)
\(x^2+5x+6-x^2-5x+2x+10=0\)
\(2x+16=0\)
\(2x=-16\)
\(x=-8\)
Mình học chật hình không giúp bạn được.Xin lỗi!



Bài 4:
a) (2x)2-2.2x.(3/2)+(3/2)2=(2x-3/2)2
b) 4(x2+2x+1)-12x-3=4x2-4x+1=(2x)2-2.2x.1+12=(2x-1)2
c) (5x)2-2.5x.2y+(2y)2=(5x-2y)2
Bài 5:
a) (x+3)3
b)[ \(\left[\left(\sqrt{3}x\right)+2\right]^3\)]
c) (3x+31)3
d) \(\left[x+\sqrt{2}y\right]^3\)


Bai cuoi cung nha ban :
goi so chinh phuong thu nhat co dang la (2n)^2 ( n khac 0 ) , so chinh phuong thu hai la (2n+2)^2 ( m khac 0 ) .
theo de bai ta co :(2n)^2 -(2m)^2=(2n-2n-2)(2n+2n+2)=4(-1)(2n+1)
vay hieu binh phuong cua hai so chinh phuong lien tiep chi het cho 4
 Giups mình với
Giups mình với

 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk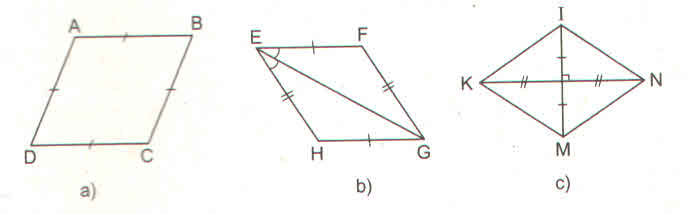













 giúp mình vs!!!
giúp mình vs!!!




`Answer:`
Câu 1:
a) \(\frac{2x+1}{6x-5}\ge\frac{3x-2}{9x-1}\)
\(\Leftrightarrow\left(2x+1\right)\left(9x-1\right)\ge\left(6x-5\right)\left(3x-2\right)\)
\(\Leftrightarrow18x-2x+9x-1\ge18x-12x-15x+10\)
\(\Leftrightarrow7x-1\ge-27x+10\)
\(\Leftrightarrow7x+27x\ge10+1\)
\(\Leftrightarrow-20x\ge11\)
\(\Leftrightarrow x\le-\frac{11}{20}\)
b) \(\frac{3}{1-x}\le\frac{3}{2x+1}\left(x\ne1;x\ne-\frac{1}{2}\right)\)
\(\Leftrightarrow\frac{3}{2x+1}-\frac{3}{1-x}\ge0\)
\(\Leftrightarrow\frac{3\left(1-x\right)-3\left(2x+1\right)}{\left(2x+1\right)\left(1-x\right)}\ge0\)
Trường hợp 1: \(\hept{\begin{cases}3\left(1-x\right)-3\left(2x+1\right)\ge0\\\left(x+1\right)\left(1-x\right)>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 0\\-\frac{1}{2}< x< 1\end{cases}}\Leftrightarrow0< x< 1\)
Trường hợp 2: \(\hept{\begin{cases}3\left(1-x\right)-3\left(2x+1\right)< 0\\\left(2x+1\right)\left(1-x\right)< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>0\\x< -\frac{1}{2}\text{ hoặc }x>1\end{cases}}\Leftrightarrow x>1\)
Câu 3:
a) Để cho giá trị của biểu thức `\frac{2x+1}{x-2}` không lớn hơn `1`
\(\Leftrightarrow\frac{2x+1}{x-2}\le1\)
\(\Leftrightarrow2x+1\le x-2\)
\(\Leftrightarrow2x-x\le-2-1\)
\(\Leftrightarrow x\le-3\)
b) Để cho giá trị của biểu thức `\frac{3x+1}{2x-1}` không bé hơn `2`
\(\Leftrightarrow\frac{3x+1}{2x-1}\ge2\)
\(\Leftrightarrow3x+1\ge2\left(2x-1\right)\)
\(\Leftrightarrow3x+1\ge4x-2\)
\(\Leftrightarrow3x-4x\ge-2-1\)
\(\Leftrightarrow-x\ge-3\)
\(\Leftrightarrow x\le3\)