K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 9 2016
A B C H E F
a/ Ta có : \(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-3^2}=3\sqrt{3}\)
Áp dụng hệ thức trong tam giác vuông : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{9}+\frac{1}{27}=\frac{4}{27}\Rightarrow AH^2=\frac{27}{4}\Rightarrow AH=\frac{3\sqrt{3}}{2}\)
b/ Dễ dàng chứng minh được AEHF là hình chữ nhật vì góc AFH = góc EAF = góc HEA = 90 độ
=> AH = EF
c/ \(EA.EB=HE^2\) ; \(AF.FC=HF^2\)
\(\Rightarrow EA.EB+AF.FC=HE^2+HF^2=EF^2=AH^2=\frac{27}{4}\)
KT
14 tháng 7 2018
A B C H
a) \(BC=BH+HC=2+6=8\)
Áp dụng hệ thức lượng ta có:
\(AH^2=BH.HC\)
\(\Rightarrow\)\(AH^2=2.6=12\)
\(\Rightarrow\)\(AH=\sqrt{12}=2\sqrt{3}\)
\(AB^2=BH.BC\)
\(\Rightarrow\)\(AB^2=2.8=16\)
\(\Rightarrow\)\(AB=4\)
\(AC^2=HC.BC\)
\(\Rightarrow\)\(AC^2=6.8=48\)
\(\Rightarrow\)\(AC=4\sqrt{3}\)
b) \(sinB=\frac{AH}{AB}=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}\)
\(cosB=\frac{BH}{AB}=\frac{2}{4}=\frac{1}{2}\)
\(tanB=\frac{AH}{BH}=\frac{2\sqrt{3}}{2}=\sqrt{3}\)
\(cotB=\frac{BH}{AH}=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}\)
29 tháng 12 2021
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
30 tháng 1 2022
a, đkxđ : a >= 0 ; a khác 9
\(P=\dfrac{2\sqrt{a}\left(\sqrt{a}-3\right)+\left(\sqrt{a}+1\right)\left(\sqrt{a}+3\right)-3-7\sqrt{a}}{a-9}\)
\(=\dfrac{2a-6\sqrt{a}+a+4\sqrt{a}+3-3-7\sqrt{a}}{a-9}=\dfrac{3a-9\sqrt{a}}{a-9}=\dfrac{3\sqrt{a}}{\sqrt{a}+3}\)
b, \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}=\dfrac{3\left(\sqrt{a}+3\right)-9}{\sqrt{a}+3}=3-\dfrac{9}{\sqrt{a}+3}\Rightarrow\sqrt{a}+3\inƯ\left(9\right)=\left\{1;3;9\right\}\)
| \(\sqrt{a}+3\) | 1 | 3 | 9 |
| a | loại | 0 | 36 |
c, Ta có : \(3=\dfrac{3\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\)mà \(3\left(\sqrt{a}+3\right)>3\sqrt{a}\)
Vậy P < 3
d, Ta có : \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}.\dfrac{\sqrt{a}-1}{\sqrt{a}}< 1\Leftrightarrow\dfrac{3\left(\sqrt{a}-1\right)}{\sqrt{a}+3}-1< 0\)
\(\Leftrightarrow\dfrac{3\sqrt{a}-3-\sqrt{a}-6}{\sqrt{a}+3}< 0\Rightarrow2\sqrt{a}-9< 0\)vì \(\sqrt{a}+3>0\)
\(\Leftrightarrow\sqrt{a}< \dfrac{9}{2}\Leftrightarrow a< \dfrac{81}{4}\)
Kết hợp đk vậy \(0\le a< \dfrac{81}{4}\)
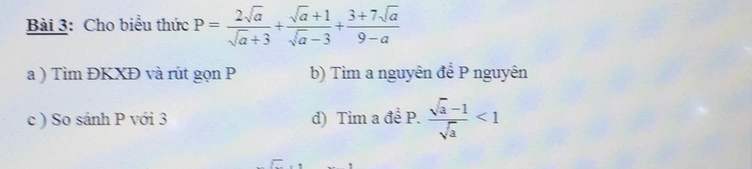
b) Ta có: \(hpt\Leftrightarrow\hept{\begin{cases}5x=5m\\2x-y=m-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=m\\2m-y=m-1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=m\\y=m+1\end{cases}}}\)
Mà x+y>1 => m+m+1>1 <=> 2m>0 <=>m>0
Vậy m>0 (Tm)