
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 5 : Gọi số táo ; cam và nho lần lượt là a ; b ; c ( quả ) ( a , b , c ∈ N* ) và lần lượt tỉ lệ với 4 ; 7 ; 9
Theo bài ra , ta có :
5a - b - c = 16
a\(\dfrac{a}{4}=\dfrac{b}{7}=\dfrac{c}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{4}=\frac{b}{7}=\frac{c}{9}=\frac{5a}{20}=\frac{5a-b-c}{20-7-9}=\frac{16}{4}\)= 4
=> a= 4.4=16
b= 4.7= 28
c=4.9=36


Bài 3 :
A B S M C P N x y 1 2 z 1 2
a) Kéo dài tia NM và NM cắt BC tại S
Khi đó ta có :
\(\hept{\begin{cases}\widehat{ABC}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\\\widehat{MNP}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\end{cases}}\Rightarrow\widehat{ABC}=\widehat{MNP}\Rightarrow\widehat{MNP}=40^o\)
b) Vẽ \(\hept{\begin{cases}\text{Bx là tia phân giác của }\widehat{ABC}\\\text{Ny là tia phân giác của }\widehat{MNP}\end{cases}}\)
\(\Rightarrow\widehat{B_1}=B_2=\widehat{N_1}=\widehat{N_2}=\frac{\widehat{ABC}}{2}=\frac{\widehat{MNP}}{2}=\frac{40^o}{2}=20^o\left(\text{do }\widehat{ABC}=\widehat{MNP}\right)\)
Vẽ Sz // Bx => \(\widehat{B_2}=\widehat{S_1}\)
Lại có \(\widehat{BSN}=\widehat{MSP}\Rightarrow\frac{\widehat{BSN}}{2}=\frac{\widehat{MSP}}{2}\Rightarrow\widehat{S_2}=\widehat{N_1}\)mà \(\widehat{S_2}\text{ và }\widehat{N_1}\)là 2 góc so le trong
=> Sz // Ny mà Sz // Bx => Bx // Ny hay tia phân giác của 2 góc \(\widehat{ABC}\text{ và }\widehat{MNP}\)song song nhau

3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

\(\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|=0\)
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|\ge0\forall x\\\left|y+\dfrac{2}{3}\right|\ge0\forall y\\\left|x^2+xz\right|\ge0\forall x;z\end{matrix}\right.\) \(\Rightarrow\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|=0\\\left|y+\dfrac{2}{3}\right|=0\\\left|x^2+xz\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{2}{3}\\z=-\dfrac{1}{2}\end{matrix}\right.\)

\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)

Bài 1:
A B C . . / D E F / // // x x
a) Xét \(\Delta AED\) và \(\Delta CEF\)có:
AE = EC (gt)
\(\widehat{AED}=\widehat{CEF}\left(đđ\right)\)
DE = EF (gt)
Do đó: \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> AD = CF (hai cạnh tương ứng)
mà AD = DB (D là trung điểm của BA)
=> CF = DB
b) Vì \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> \(\widehat{DAE}=\widehat{FCE}\) (hai cạnh tương ứng)
=> DA // CF
mà D nằm giữa đoạn thẳng AB (D là trung điểm của AB)
=> DB // CF
=> \(\widehat{BDC}=\widehat{FCD}\left(soletrong\right)\)
Xét \(\Delta BDC\) và \(\Delta FCD\) có:
DC (chung)
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
BD = CF (cmt)
Do đó: \(\Delta BDC=\Delta FCD\left(c-g-c\right)\)
c) Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> \(\widehat{BCD}=\widehat{FCD}\) (hai cạnh tương ứng)
=> DF // BC (soletrong)
hay DE // BC
Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> DF = BC (hai cạnh tương ứng)
mà \(DE=\dfrac{1}{2}DF\) (D là trung điểm của DF)
=> \(DE=\dfrac{1}{2}BC\)

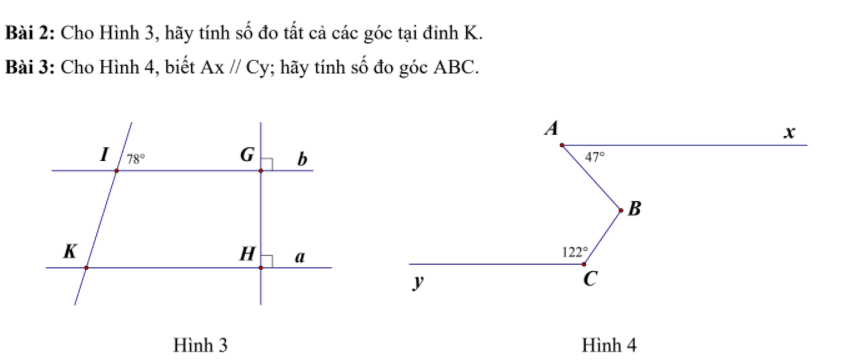

 Tớ Đang Cần giải bài này gấp mai tớ phải gửi bài giúp tớ với
Tớ Đang Cần giải bài này gấp mai tớ phải gửi bài giúp tớ với



 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ





 GIÚP VỚI CẦN GẤP LẮM !!!
GIÚP VỚI CẦN GẤP LẮM !!! 



Bài 2:
Vì $b\perp GH, a\perp GH\Rightarrow a\parallel b$
Do đó:
$\widehat{K_1}=\widehat{I_1}=78^0$ (hai góc đồng vị)
$\widehat{K_2}=\widehat{K_1}=78^0$ (hai góc đối đỉnh)
$\widehat{K_4}=180^0-\widehat{K_1}=180^0-78^0=102^0$ (hai góc kề bù)
$\widehat{K_3}=\widehat{K_4}=102^0$ (đối đỉnh)
Bài 3: Kẻ tia $Bt\parallel Ax$. Vì $Ax\parallel Cy$ nên $Bt\parallel Cy$
Ta có:
$\widehat{B_1}=\widehat{BAx}=47^0$ (hai góc so le trong)
$\widehat{B_2}+\widehat{BCy}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{B_2}=180^0-\widehat{BCy}=180^0-122^0=58^0$
Do đó: $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=47^0+58^0=105^0$