Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời : Bài làm
Đổi :\(1h20p=\frac{4}{3}h\)
Vận tốc thực của cano là:30-5=25 (km/h)
Gọi x là độ dài từ A đến B
Thời gian cano xuôi dòng là:\(\frac{x}{25+5}h\)
Thời gian cano ngược dòng là: \(\frac{x}{25-5}h\)
Từ đó ta có pt: \(\frac{x}{20}-\frac{x}{30}=\frac{4}{3}\)
Giải ra được \(x=80km\)
Mk ko chắc
Tk mk nha

Gọi vận tốc của ca nô lúc dòng nước yên lặng là x (km/h); (x > 2)
Vì vận tốc nước là 2 km/h nên vận tốc xuôi dòng và ngược dòng lần lượt là x + 2 và x – 2 (km/h)
Thời gian để ca nô đi hết 42 km xuôi dòng là 42/(x+2) (h)
Thời gian để ca nô đi hết 20 km ngược dòng là 20/(x-2) (h)
Tổng thời gian là 5h do đó
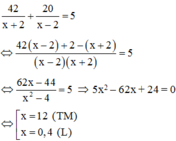
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h
Đáp án: B

Gọi vận tốc thực tế của ca nô là x ( km/h ) ( x > 0 )
Vận tốc của ca nô khi xuôi dòng là: \(x+4\)( km/h ) ( lấy vận tốc ca nô + với vận tốc nước )
Thời gian xuôi dòng của ca nô là: \(\frac{30}{x+4}\)( giờ )
Vận tốc ngược dòng của ca nô là: \(x-4\)( km/h ) ( lấy vận tốc ca nô - với vận tốc nước )
Thời gian ngược dòng của ca nô là: \(\frac{30}{x-4}\)( giờ )
Theo đề bài ta có phương trình:
\(\frac{30}{x+4}+\frac{30}{x-4}=4\)
Giải nốt cái phương trình rồi kết luận
Toán lớp 5 kì 2 , ko phải toán lớp 9 => bịa là toán 9 => ko làm

Gọi vận tốc của ca nô khi nước yên lặng là x (km/h) (Điều kiện: x > 2)
Vận tốc của ca nô khi xuôi dòng là: x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng là: x - 2 (km/h)
Thời gian ca nô đi xuôi dòng là: \(\frac{42}{x+2}\left(h\right)\)
Thời gian ca nô đi ngược dòng là: \(\frac{20}{x-2}\left(h\right)\)
Vì tổng thời gian xuôi dòng và nược dòng là 5 giờ do đó ta có phương trình:
\(\frac{42}{x+2}+\frac{20}{x-2}=5\)
Giải phương trình, ta có: \(5x^2-62x+24=0\)
Ta được: \(x=12\) (km/h)
Vậy vận tốc của ca nô khi nước yên lặng là: 12 km/h

*Gọi vận tốc riêng của thuyền là x (km/h) (1<x < 60)
Vận tốc khi xuồng xuôi dòng là: x + 1 (km/h)
Vận tốc khi xuồng ngược dòng là: x - 1(km/h)
*Thời gian xuồng xuôi dòng từ A --> B là: 60/(x + 1) (h)
Thời gian xuồng xuôi dòng đến bến C là: 25/(x - 1) (h)
30 phút = 1/2 (h)
*Vì thời gian kể từ lúc đi đến lúc quay trở lại đến bến C hết tất cả là 8 giờ nên ta có PT:
60/(x + 1) + 25/(x - 1) + 1/2 = 8
=> 60.2.(x - 1) + 25.2(x + 1) + (x - 1)(x + 1) = 8.2(x - 1)(x + 1)
<=> 120x - 120 + 50x + 50 + x^2 - 1 = 16x^2 - 16
<=> 15x^2 - 170x + 55 = 0
delta' = (- 85)^2 - 55.15 = 6400 = 80^2 > 0
=> PT có 2 nghiệm pb:
x1 = (85 - 80)/15 = 1/3 (loại)
x2 = (85 + 80)/15 = 11 (thỏa mãn điều kiện bài ra)
Vậy vận tốc xuồng máy khi nước yên lặng là 11km/h
Bài 10:
Gọi số thứ nhất là x(0<x<19)x(0<x<19)
Vậy số thứ hai là 19−x19−x
Theo đề x2+(19−x)2=185⇔x2−19x+88=0x2+(19−x)2=185⇔x2−19x+88=0
Vậy hai số cần tìm là 11 và 8
Bài 10:
Gọi 2 số cần tìm là a;b. Ta có: a+b=19 và a2+b2=185
(a+b)2=192 <=> a2+2ab+b2=361 <=> 2ab+185=361 <=> 2ab=176 <=> ab=88
Ta có hệ pt \(\hept{\begin{cases}a+b=19\\ab=88\end{cases}}\)
Giải cái đó ra bạn sẽ tìm được a;b