
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=30+31+32+.......+32009
2A=31+32+............+32010
2A-A=(31+32+..........+32010)-(30+31+........+32009)
A=32010-30
A=32010-1
Cứ 1 nhóm có 4 số(3x3x3x3)=1
2010:4=502(dư 2)
Vì còn dư 2 =>3x3=9
Vậy tích trên có chữ số tận cùng là:
..........9-1=.........8
Vậy A chia hết cho 8
đặt A như đề bài ta có kết quả như bn Dũng
A bằng \(3^{2010}-1\)
Ta có \(3^{2010}\)bằng \(9^{1005}\)
Mà \(9\)đồng dư vs \(1\)(mod 8)
\(\Rightarrow9^{1005}\)đồng dư vs \(1^{1005}\)(mod 8)
\(\Rightarrow9^{1005}\)đồng dư vs \(1\)(mod 8)
\(\Rightarrow9^{1005}-1\)đồng dư vs \(0\)(mod 8)
Vậy A chia hết cho 8



ab/2 = 2(a + b + c)
ab/4 = a + b + c
(ab/4 - a - b)2 = c2
Theo Pytago ta có a2 + b2 = c2.
Suy ra (ab/4 - a - b)2 = a2 + b2
a2b2/16 + a2 + b2 + 2ab - a2b/2 - ab2/2 = a2 + b2
a2b2/16 - a2b/2 - ab2/2 + 2ab = 0
ab(ab/16 - a/2 - b/2 + 2) = 0
Vì ab ≠ 0 nên ta có ab - 8a - 8b + 32 = 0.
Hay ab - 8a - 8b + 64 - 32 = 0
a (b - 8) - 8(b - 8) = 32
(a - 8)(b - 8) = 32 = 1 x 32 = 8 x 4 = 2 x 16.
Các cặp (a - 8; b - 8) tương ứng là (1; 32), (8; 4), (2; 16).
Suy ra các cặp (a; b) tương ứng là (9; 40), (16; 12) và (10; 24). Từ đó suy ra c tương ứng trong các trường hợp lần lượt là 41; 20 và 26.
Vậy, các trường hợp của tam giác vuông có cạnh (a; b; c) thỏa mãn đề bài là
(9; 40; 41); (16; 12; 20) và (10; 24; 26).
Vì diện tích tam giác bằng 2 lần chu vi ta có :
\(\frac{ab}{2}=2\left(a+b+c\right)\)
\(\frac{ab}{4}=a+b+c\)
\(\left(\frac{ab}{4}-a-b\right)^2=c^2\)
Theo đeịnh lý PITAGO :
\(a^2+b^2=c^2\)\(\Rightarrow\)\(\left(\frac{ab}{4}-a-b\right)^2=a^2+b^2\)
\(\frac{a^2b^2}{16}+a^2+b^2+2ab-\frac{a^2b}{2}-\frac{ab^2}{2}=a^2+b^2\)
\(\frac{a^2b^2}{16}-\frac{a^2b}{2}+2ab=0\)
\(ab\left(\frac{ab}{16}-\frac{a}{2}-\frac{b}{2}+2\right)=0\)
Hay \(ab-8a-8b+32=0\)
\(a\left(b-8\right)-8\left(b-8\right)=32\)
\(\left(a-8\right)\left(b+8\right)=32=32.1=8.4=16.2\)
Các cặp ( a - 8 ; b - 8 ) tương ứng là ( 1 ; 32 ) ; ( 8 ; 4 ) ; ( 2 ; 16 )
Suy ra các cặp ( a ; b ) tương ứng là ( 9 ; 14 ) ; ( 16 ; 12 ) ; ( 10 ; 24 ) . Suy ra c tương ứng trong các trường hợp là 41 ; 20 và 26
Vậy các trường hợp của tam giác vuông có cạnh ( a ; b ; c ) thỏa mãn đề bài là ( 9 ; 40 ; 41 ) ; ( 16 ; 12 ; 20 ) ; ( 10 ; 24 ; 26 )

a/b=c/d =>a/c=b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)\(\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left(\frac{a+b}{b+d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow dpcm\)

a) \(\left(-\dfrac{2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
= \(\left(-\dfrac{2}{3}+\dfrac{3}{7}-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
= \(0:\dfrac{4}{5}\)
= 0
b) \(\dfrac{5}{9}\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
= \(\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}+\dfrac{1}{15}-\dfrac{2}{3}\right)\)
= \(\dfrac{5}{9}:-\dfrac{81}{110}\)
= \(-\dfrac{550}{729}\)
Giải:
a) \(\left(\dfrac{-2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left[\left(\dfrac{-2}{3}+\dfrac{2}{7}\right)+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right)\right]:\dfrac{4}{5}\)
\(=\left(\dfrac{-2}{3}+\dfrac{2}{7}-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left(-1+1\right):\dfrac{4}{5}\)
\(=0:\dfrac{4}{5}\)
\(=0.\dfrac{4}{5}\)
\(=0\)
b) \(\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
\(=\dfrac{5}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)\)
\(=\dfrac{5}{9}:\dfrac{-3}{22}+\dfrac{5}{9}:\dfrac{-3}{5}\)
\(=\dfrac{5}{9}:\left(\dfrac{-3}{22}-\dfrac{3}{5}\right)\)
\(=\dfrac{5}{9}:\left(\dfrac{-3}{22}-\dfrac{3}{5}\right)\)
\(=\dfrac{5}{9}:\dfrac{-81}{110}\)
\(=-\dfrac{550}{729}\)
Chúc bạn học tốt!!!




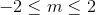 B.
B. 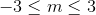
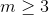






I don't know
Khó quá vậy